[Algorithm] Algorithm DP1
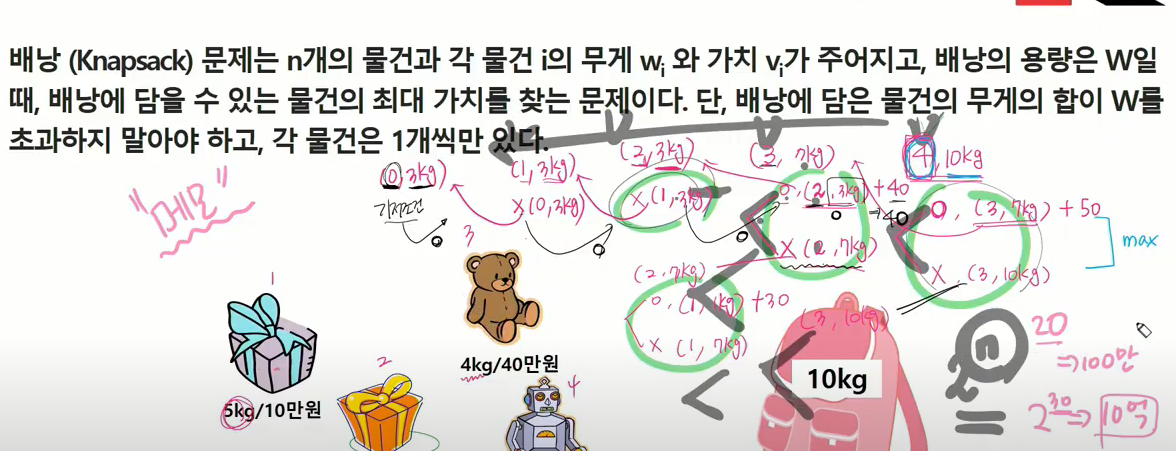


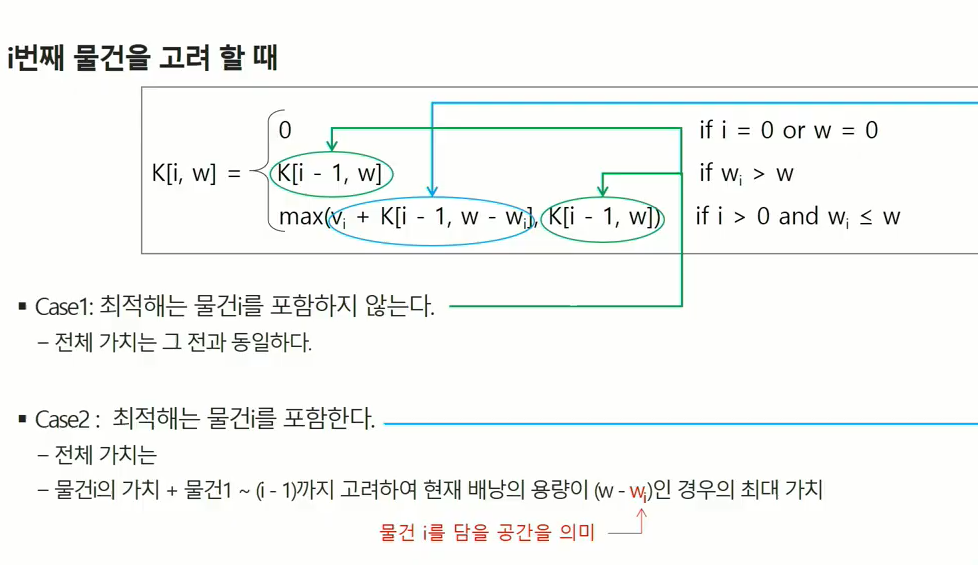
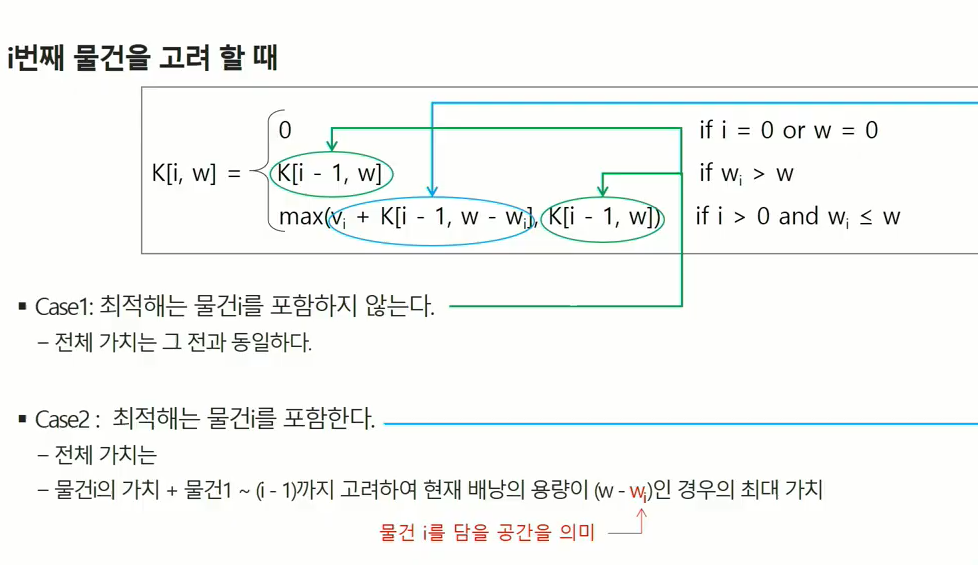
초록색은 최적해를 따지는 부분에 물건 i 포함 안아는 경우
하늘색은 최적해를 따지는 부분에 물건 i를 고려한 경우
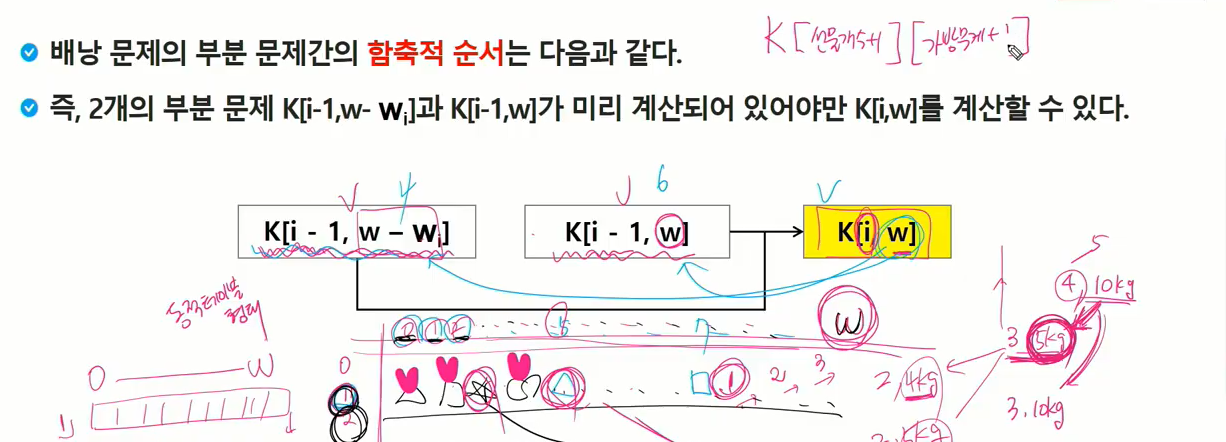
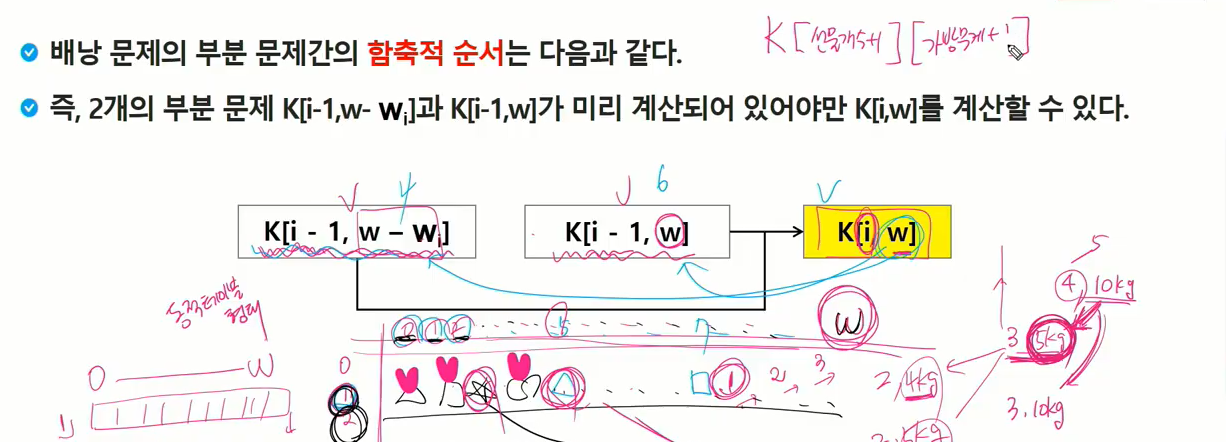
DP로 풀어내려면 구해진 부분문제의 해가 다음 문제 해결하는데 쓰일 수 있는 부분문제의 해이면서 최적화 적용
i번쨰 물건까지 w무게 만족하는 최적과정에서 그 전의 내용을 사용하는 과정이 나왔다. w 만드는 가치 구하기 전에 i-1까지 w-W,w 만족하는 계산이 미리 되어 있으면 i물건까지 w무게 만족하는 최적의 가치 구할 수 있다.
package com.ssafy;
import java.util.Scanner;
public class DP_KnapsackTest {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int W = sc.nextInt();
int [] weights = new int[N+1];//물건의 무게정보
int [] profits = new int[N+1];//물건의 가치 정보
int [][]D = new int[N+1][W+1];//해당 물건까지 고려하여 해당 무게를 만들 떄의 최대 가치
for(int i =1; i<=N;i++) {
weights[i] = sc.nextInt();
profits[i] = sc.nextInt();
}
for(int i =1; i<=N;i++) { //첫 물건부터 고려
for(int w = 1; w<=W;W++)// 무게 1부터 고려
{
if(weights[i]<=w) {//가방에 넣을 수 있는 상황
//넣을까
Math.max(D[i-1][w-weights[i]]+profits[i],D[i-1][w]); //자신이 들어가면서 생기는 가치.
//말까
D[i][w] = D[i-1][w];
}else { //가방에 넣지 못하는 상황
D[i][w] = D[i-1][w];
}
//시간복잡도는? for 2번 돌면서 위에거 실행한다 치면 n2
//근데 재귀적이면 물건이 30개만 되도 2의 30승이였다. 굉장히 큰 차이.
//계산하는 과정에서 어떤 무게가치들이 쓰일지 모른다.
//사용되지 않은 애들도 있음. 뒤쪽에서 안 쓰일 수 있음. DP도 다 계산하는데 스마트하게 다한다(스마트한 완탐)
}
}
System.out.println(D[N][W]);
}
}
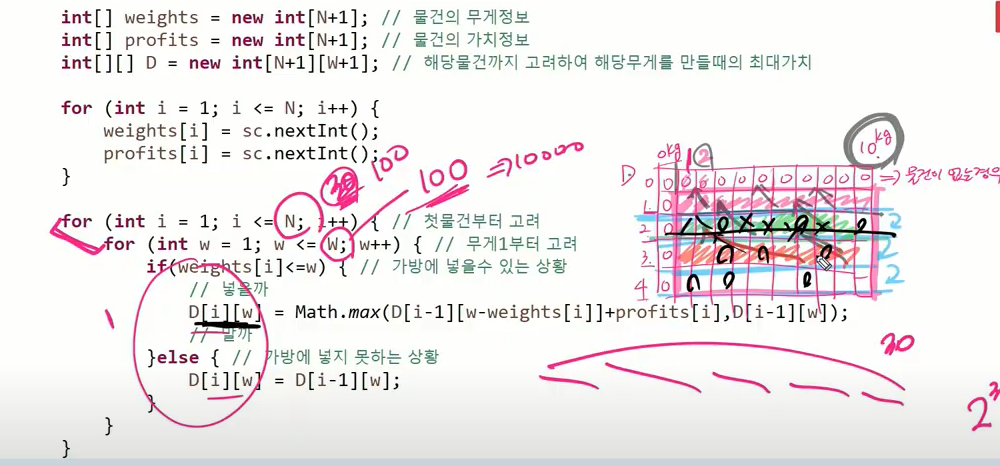
시간복잡도는? for 2번 돌면서 위에거 실행한다 치면 n2 근데 재귀적이면 물건이 30개만 되도 2의 30승이였다. 굉장히 큰 차이. 계산하는 과정에서 어떤 무게가치들이 쓰일지 모른다. 사용되지 않은 애들도 있음. 뒤쪽에서 안 쓰일 수 있음. DP도 다 계산하는데 스마트하게 다한다(스마트한 완탐)
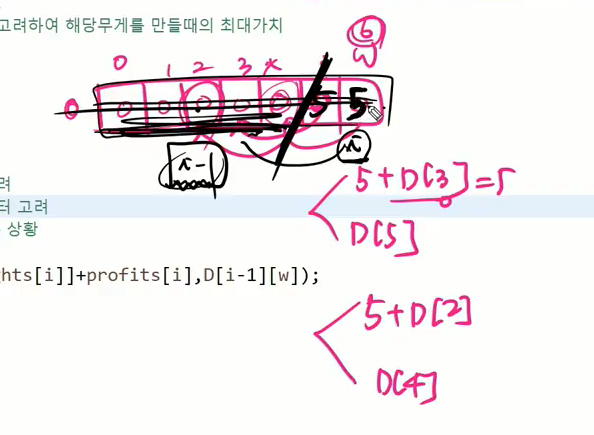
배열은 근데 1차원으로도 가져갈 수 있다.
어려운 게 맞다. 그래도 보고 또보고 해서 낮선 느낌이 없어지면 그래도 한 발 전진했다고 볼 수 있다.
최장 증가 수열(LIS)
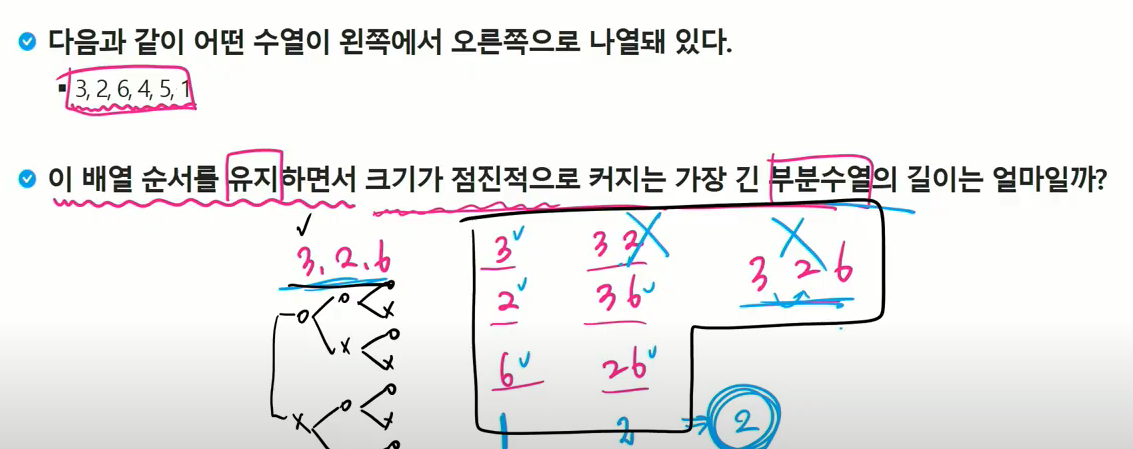
-> 수열 모든 부분집합을 구해 그 부분집합이 증가수열인지 판별한다. 증가 수열 중 가장 길이가 긴 값을 구한다.
냅색도 그렇고 lis도 그렇고 항상 넣을까 말까를 고려한다
DP는 수도코드 그대로 구현하면 끝이다.

맨 끝인 6의 길이가 필요한 게 아니라 전부 끝이 될 수 있고 그중 가장 길이가 긴 LIS를 선택.
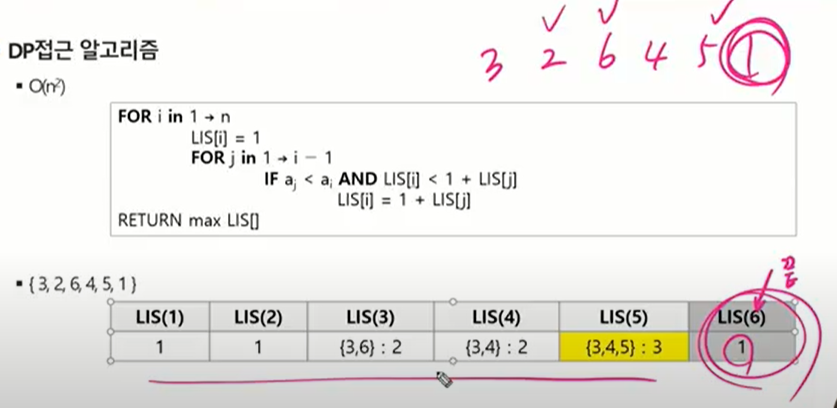
반복돌면서 가장 큰 값 찾던지.
package com.ssafy;
import java.util.Arrays;
import java.util.Scanner;
public class DP_ListTest {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int [] arr = new int[N];//원소들 저장
int[] LIS = new int[N]; //각 원소를 마지막에 세웠을 때의 최장길이
for(int i =0; i<N;i++) {
arr[i] = sc.nextInt();
}
// Arrays.fill(LIS, 1);
int max=0; //하나씩 값 돌때마다 max 갱신하게
for(int i =0; i<N; i++) {
LIS[i]=1;//어차피 반복 돌리니까 그냥 안에서 직접 돌리자.
//자기 혼자 세웠을 떄의 길이로 초기화
for(int j =0; j<=i-1;j++) { //맨 앞부터 자신의 직전의 원소들과 비교
if(arr[j]<arr[i] && LIS[i]<LIS[j]+1) {
LIS[i] = LIS[j]+1;
}
}
if(max<LIS[i]) max = LIS[i];
}
System.out.println(max);
/* 4 1 4 3 2*/
// N2을 NlogN으로 바꾸기만 해도 대박.
// N이 10만이면 N2은 100억
// NlogN은 10만에 대한 log10만
}
}

N2을 NlogN으로 바꾸기만 해도 대박. N이 10만이면 N2은 100억 NlogN은 10만에 대한 log10만
그래서 이 N2를 NlogN으로 바꿔보자.
하나는 IM 수준 하나는 ADV 수준 냅색 , 거스름돈 ,배달할 떄 밀가루봉지문제 문제 테스트 케이스는 통과 되도 히든테케도 통과되게해야.(최적화 해야한다.) IM은 정렬한다던가. 조합 쓴다던가 순열 쓴다던가 부분집합 쓴다던가. 가장 만만한게 배열로 인덱스를 맘대로 접근해서 사방, 팔방탐색하는게 가장 단순할 수도. IM이 그래프 탐색 이런거 나오지는 않을거라 생각.
방식 어쨌건 답이 나오면 됨. 일단 결과만 나오면 됨. 최적화 못해서 추가점수 없을 수도 있지만 IM은 답만 일단 나오면 됨.
수가 여러개 = 수열
LIS : 원소가 n개인 배열의 일부 원소를 골라내서 부분 수열을 만들었을 떄 각각의 원소는 이전 원소보다 더 크다는 조건을 만족하 길이가 최대인 부분수열.
LIS[n]:전체 수열의 n번째 값까지 고려했을 때 만들어지는 최장 수열의 길이.
어떤 기준이 되는 애가 있을떄 앞에서 증가가 되는 거로 왔다 5 입장에선 앞에 4개가 있다. 앞에 조건 만족하는거 뒤에 붙이면 자기 포함해서 최장증가 되는걸 만족.
하지만 맨 처음에는 기준이 되는 애가 있을 떄 앞에 오는 애가 어떻게 될 지 모르고 뒤에 오는 애가 어떻게 될 지 모르기 떄문에 해당 숫자로 만들 수 있는 최장은 자기 자신만일 수도 있다.
DP로 풀어보기 (LIS)
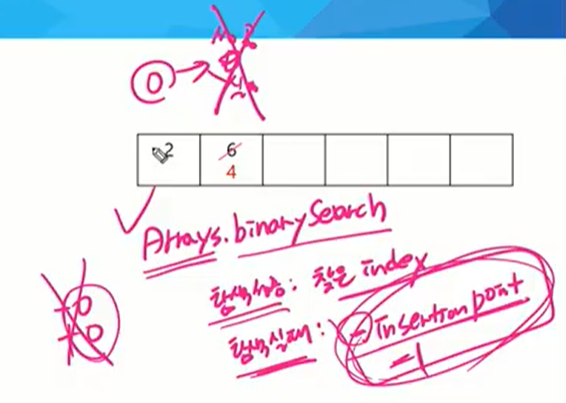
LIS에선 원소 순서 바꾸면 안됨 () 삽입 될 수 있는 자리 찾기 정렬된 결과 유지 정렬된 집합 = 원소 빠르게 탐색.(이진 탐색)
모든 쌍 최단 경로
다익스트라를 여러번 돌리면 된다.
N번 돌리면 N3임. 다익스트라가 단순한 n2이 아니라 N2보다는 좀 완화된 N log N과 비슷하게 보일 수 있도록 이걸 돌리면 N2의 log N이 된다.
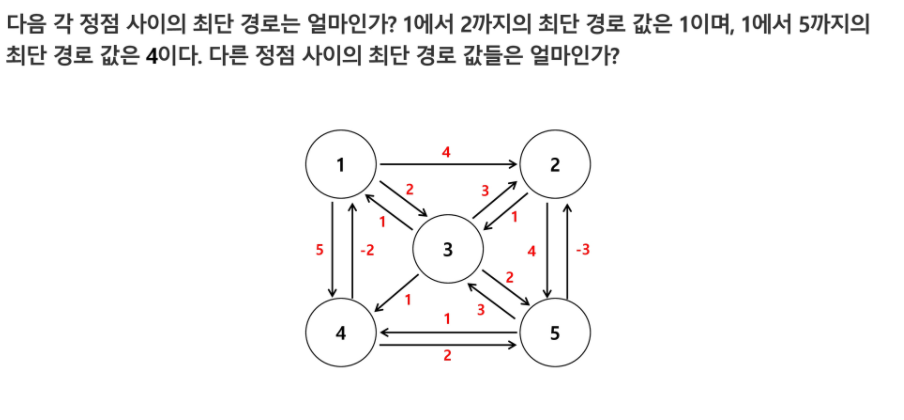
최단 경로
- 한 도시에서 다른 도시로 가장 빨리 갈 수 있는 경로를 찾는 문제
- 가중치 포함, 방향성 그래프에서 최단경로 찾기
- 최적화 문제 -> 주어진 문제에 대해 하나 이상의 많은 해답이 존재할 때, 이 가운데에서 가장 최적인 해답을 찾아야 하는 문제.
3중 포문 돌긴 도는데 모든쌍의 최단경로경우 구하기 위해서 모든 쌍의 대한 반복을 돌리면서 경유지를 계속 변화주면서 값을 구해간다.

이게 헷갈리면 경찰과 도둑 으로 외우자…
brute-force 접근 방법
- 한 정점에서 다른정점으로의 모든 경로를 구한 뒤, 그들 중에서 최단 경로를 찾는다.
- 그래프가 n개의 정점을 가지고 있고, 완전그래프라고 가정하면, 한 정점 i에서 어떤 정점 j로 가는 경로들을 다 모아보면, 그 경로들 중에서 나머지 모든 정점을 한번씩은 꼭 거쳐서 가는 경로들도 포함되어 있는데, 그 경로들의 수만 우선 계산해보자
i에서 출발하여 처음에 도착할 수 있는 정점의 가지 수는 n-2 개이고 그 중에 하나를 선택하면, 그 다음에 도착할 수 있는 정점의 가지수는 n-3개이고, 이렇게 계속해서 계산해보면, 총 경로의 개수는 (n-2)(n-3)..1 = (n-2)!이 된다.
- 이 경로의 개수만 보아도 지수보다 훨씬 크므로 이 알고리즘은 절대 비효울적이다.
DP 접근방법
이 문제를 해결하려면 , 각 점을 시작점으로 정해 다익스트라의 최단경로 알고리즘을 수행하면 된다.
이때의 시간 복잡도는 인접행렬을 사용하면 O(n3)이다. 단 n은 정점의 수이다.
워셜은 그래프에서 모든 쌍의 경로존재여부를 찾아내는 동적계획 알고리즘을 제안했고 , 플로이드는 이를 변형하여 모든 쌍 최단경로를 찾는 알고리즘을 고안하였다.
즉, 모든 쌍 최단경로를 찾는 동적 계획 알고리즘을 플로이드-워셜 알고리즘이라 한다.
- 플로이드 알고리즘의 시간복잡도는 O(n3)으로 다익스트라의 시간복잡도와 동일하다.
- 그러나 플로이드 알고리즘은 매우 간단하여 다익스트라 알고리즘을 사용하는 것 보다 효율적이다.
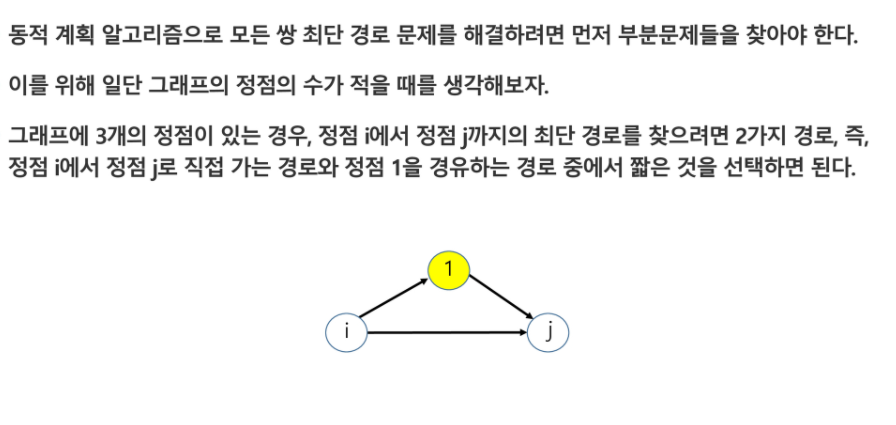
2번만 경유지로 쓰는게 아니라 경유지를 추가
경유지를 바꾸는데 직접비용과 비교하는게 아니라 n-1번째로 추가하는 경유지라면 정점인 n-1까지 다 비교했을떄 비교
경유지를 늘려간다고 생각해야 한다.
하나의 중요한 아이디어는 경유가능한 정점들
- 정점 1로 시작하여, 정점1과 2 그다음엔, 정점 1,2,3으로 하나씩 추가하여 마지막엔 정점 1~n까지의 모든 정점을 경유 가능한 정점들로 고려하면서 , 모든 쌍의 최단 경로의 거리를 계산한다.
부분 문제 정의 : 단, 입력 그래프의 정점을 각각 1,2,3,…,n이라 하자.
- Dk = 정점{1,2,3,…,k} 만을 경유 가능한 정점들로 고려하여, 정점 i로부터 정점 j까지의 모든 경로 중에서 가장 짧은 경로의 거리
여기서 주의해야 할 것은 정점 1에서 정점 k 까지의 모든 정점들을 반드시 경유하는 경로를 의미하는 것이 아니다.
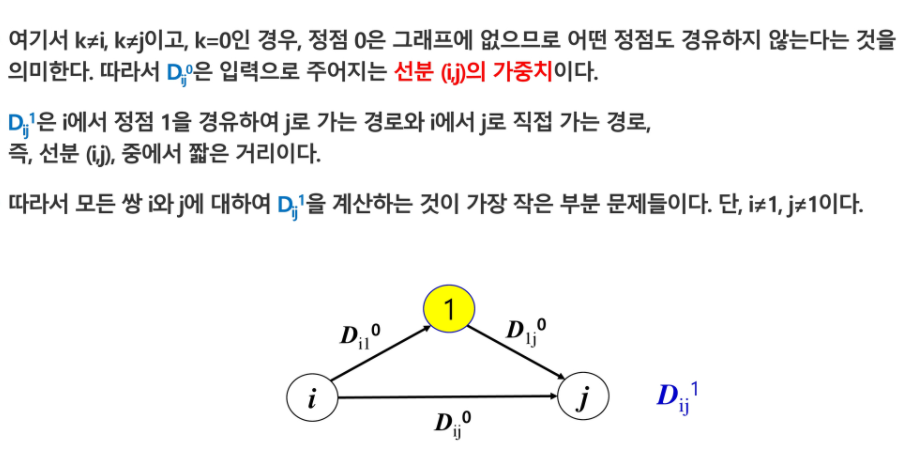
i에서 j까지 최단경로만 구하는 게 아니라 모든 쌍에 대한 최단 경로를 다 구해야 한다.
사실 플로이드 워셜은 코드는 짧아서 금방 짜는데 저 원리와 과정을 이해하는게 더 중요하다.
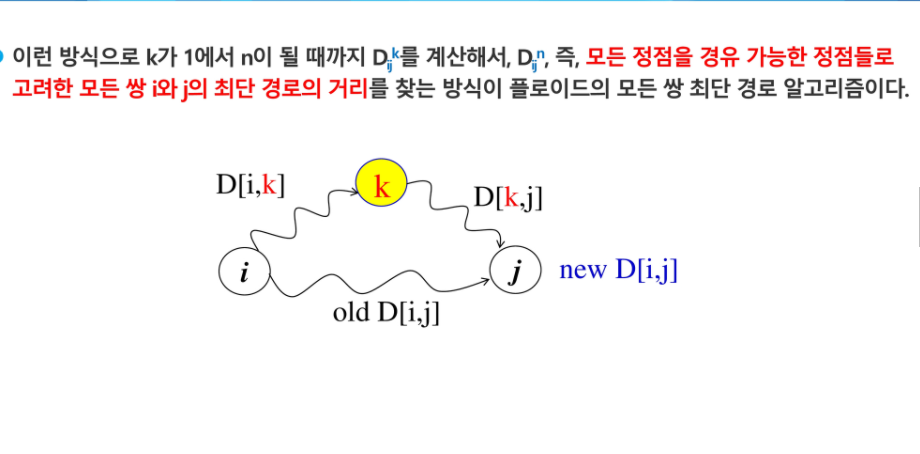

거쳐오지 않는게 유리할 수 있고 거쳐오는게 유리할 수 있으니 그 중 최소값을 D[i][j]에 넣는다.
1을 띄워서 돌려보고 2띄워서 돌려보고 이렇게 1에서 1가고 1에서 2가고 13가고 14가고 다 구하는거.
배열이 분홍색만 칠해진다.
1번 정점에서 다른 애들한테 가는 최소값이 저장 그리고 출발지 2로 바꾸면 밑에도 그 2부분만 업데이트 하려고 시도. 근데 이 과정에서 경유지에 쓰는 값이 하늘색 부분인 밑에도 쓰면?(아직 최적이 아닌 값) 그걸 이용해서 최적해 결정하고 다 채우면 절대 업데이트 안 일어나서 오답이 나오게 된다.
그래서 우린 모든 쌍을 동등한 입장에서 고려(어떤건 경유지1개 고려하는데 어떤건 2,3개 고려하면 안됨) 어떤 애든 동등한 조건에서 고려해야한다. 모든 쌍에 관련된 최단을 업데이트 하고 모든해에 대해 최단 구한다.
어떤 위치에서 뭘 쓰더라도 직전 단계의 최적해를 보장하게 해야.
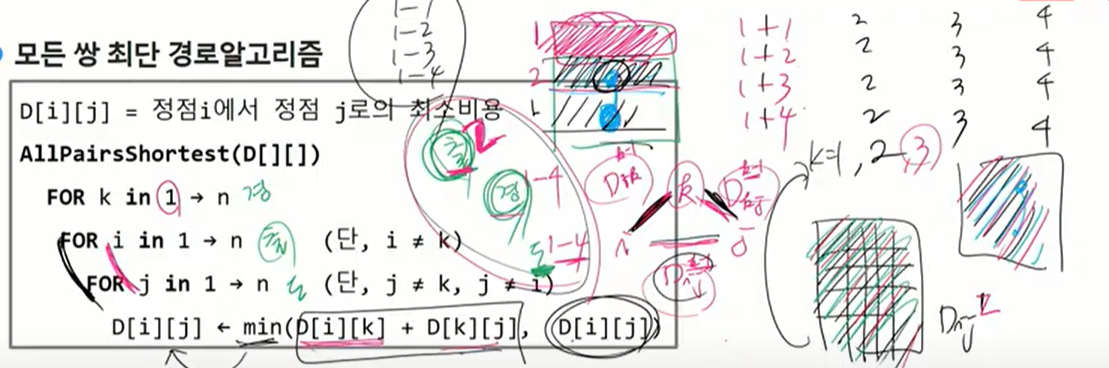
핵심은 한번씩 경유지가 늘어날 때마다 각 위치는 그 경유지까지 고려한 최단경로가 된다고 생각 할 수 있다.
코드 볼때는 짧았는데 막상 설명 들으면 어렵다.(당연. trade-off라 생각하자.)