크루스칼 과정

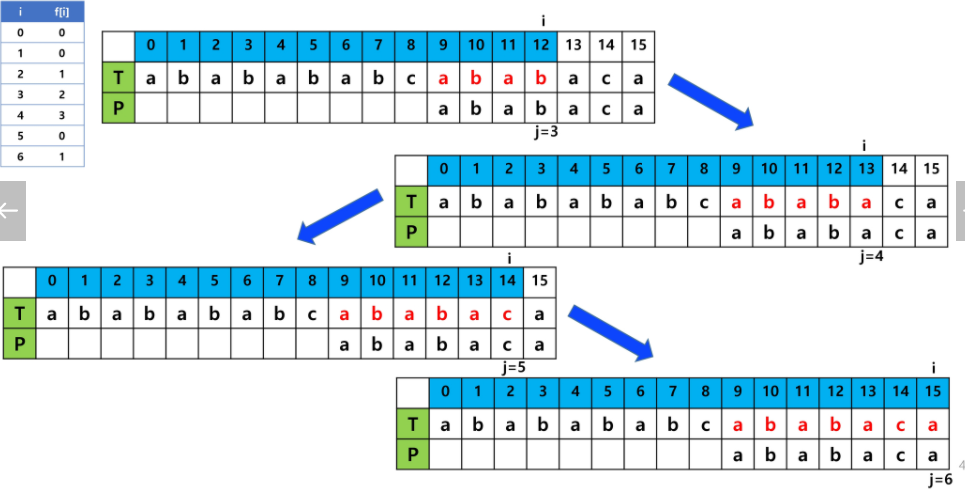
DP1

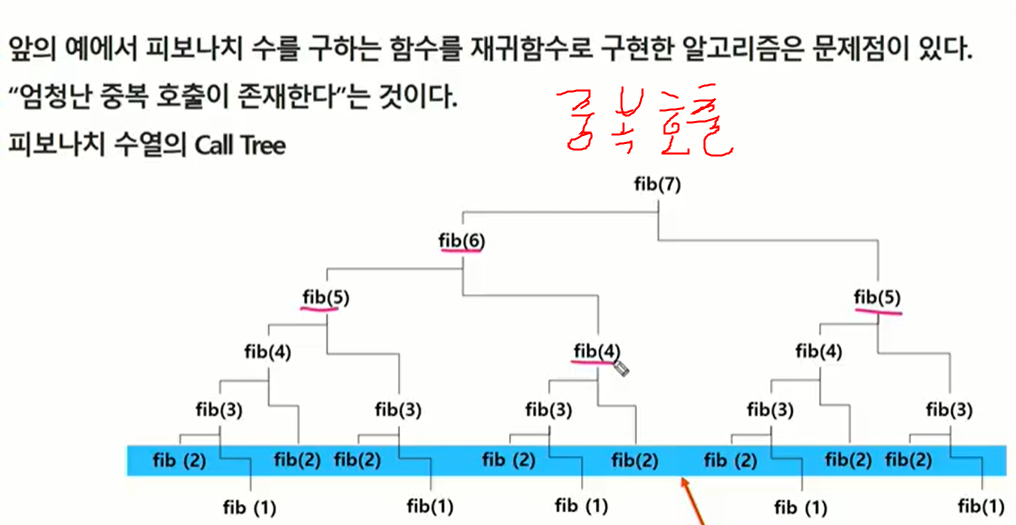
메모이제이션

• 메모이제이션(memoization)은 컴퓨터 프로그램을 실행할 때 이전에 계산한 값을 메모리에 저장해서 매번 다시 계산하지 않도록 하여 전체적인 실행속도를 빠르게 하는 기술이다. 동적 계획법의 핵심이 되는 기술이다.

• 메모이제이션은 글자 그대로 해석하면 “메모리에 넣기”라는 의미이며 기억해야 할 것이라는 뜻.

메모이제이션은 추가적인 메모리 공간이 필요하다 재귀함수 호출로 인한 시스템 호출 스택을 사용하게 되고 실행속도 저하 또는 오버플로우가 발생할 수 있다.

동적 계획법

동적계획법은 그리디 알고리즘과 같이 최적화 문제를 해결하는 알고리즘이다.(스마트한 완탐)

• 최적화 문제 : 최적(최대값이나 최소값 같은) 값을 구하는 문제

  해당 문제에 여러 해가 있을 수 있다.

• 동적 계획법은 먼저 작은 부분 문제들의 해들을 구하고 이들을 이용하여 보다 큰 크기의 부분 문제들을 해결하여, 최종적으로 원래 주어진 문제들을 해결하는 알고리즘 설계기법이다.

중복 부분문제구조

• DP는 큰 문제를 이루는 작은 문제들을 먼저 해결하고 작은 문제들의 최적해를 이용하여 순환적으로 큰 문제를 해결한다. -> 순환적인 관계를 명시적으로 표현하기 위해 동적 계획법에서는 일반적으로 수학적인 도구인 점화식을 사용한ㄷ.

• DP는 문제의 순환적인 성질 때문 이전에 계산되어졌던 작은 문제의 해가 다른 어딘가에서 필요하게 되는데 이를 위해 DP에선 이미 해결된 작은 문제들의 해를 어떤 저장공간에 저장하게 된다.

• 그리고 이렇게 저장된 해들이 다시 필요할 때 마다 해를 얻기 위해 다시 문제를 재계산 하지 않고 테이블의 참조를 통해 중복된 계산을 피하게 된다.

최적 부분 문제 구조

• 동적 계획법이 최적화에 대한 어느 문제나 적용 될 수 있는 건 아니다. 주어진 문제가 최적화의 원칙을 만족해야만 동적 계획법을 효율적으로 적용할 수 있다.

• 최적화의 원칙이란 어떤 문제에 대한 해가 최적일 떄 그 해를 구성하는 작은 문제들의 해 역시 최적이어야 한다는 것.

• 동적 계획법 자체가 큰 문제의 최적해를 작은 문제들의 최적해들을 이용해 구하기 떄문에 만약 큰 문제의 최적해가 작은 문제들의 최적해로 구성되지 않으면 이 문제는 동적계획법을 구성할 수 없다.

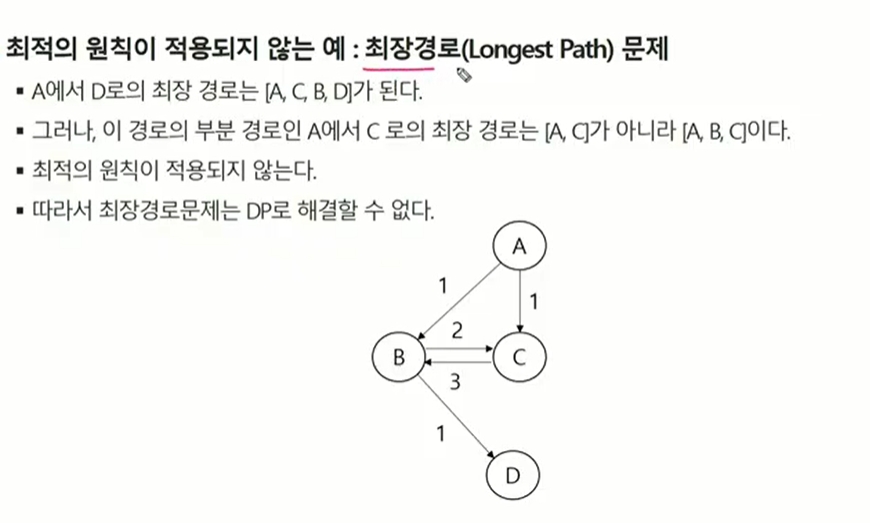
최장경로는 최소 원칙 적용 안됨.

분할정복과 동적 계획법의 비교

분할정복

1. 연관없는 부분문제로 분할한다.
2. 부분문제를 재귀적으로 해결한다.
3. 부분문제의 해를 결합한다. ex) 병합정렬, 퀵정렬

DP

1. 부분문제들이 연관이 없으면 적용할 수 없다. 즉 부분문제들은 더 작은 부분문제들을 공유한다.
2. 모든 부분문제를 한번만 계산하고 결과를 저장하고 재사용한다.

• DP에는 부분문제들 사이에 의존적 관계가 존재한다.

• 이러한 관계는 문제에 따라 다르고 대부분의 경우 뚜렷이 보이지 않아서 함축적인 순서라고 한다.

• 분할정복은 하향식 방법으로 DP는 상향식 방법으로 접근한다.

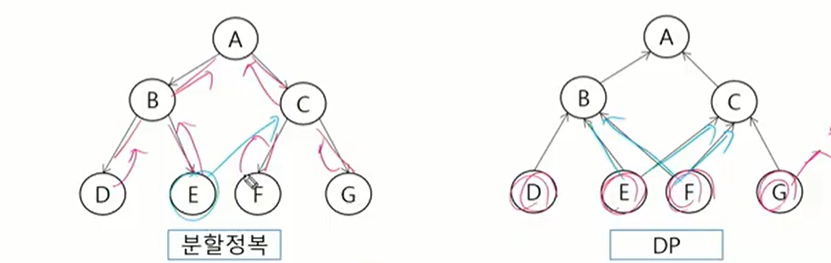
DP 적용 접근 방법

• 최적해 구조의 특성을 파악하라 -> 문제를 부분문제로 나눈다.

• 최적해의 값을 재귀적으로 정의하라 -> 부분 문제의 최적해 값에 기반하여 문제의 최적해 값을 정의한다.

• 상향식 방법으로 최적해의 값을 계산하라. -> 가장 작은 부분문제부터 해를 구한 뒤 테이블에 저장한다. -> 테이블에 저장되어 있는 부분문제의 해를 이용하여 점차적으로 상위 부분문제의 최적해를 구한다(상향식 방법)

다이나믹 프로그래밍

• 다이나믹 프로그래밍에서 각각의 작은 문제는 한번만 풀기
• optimal substructure를 만족하기 때문에 같은 문제는 여러번 풀어도 답이 같음.
• 그러므로 답을 한번 구하면 저장해놓기 => Memoization

다이나믹 프로그래밍 풀이방법

1. Top-down:재귀이용
2. Bottom-up: 반복문 이용.

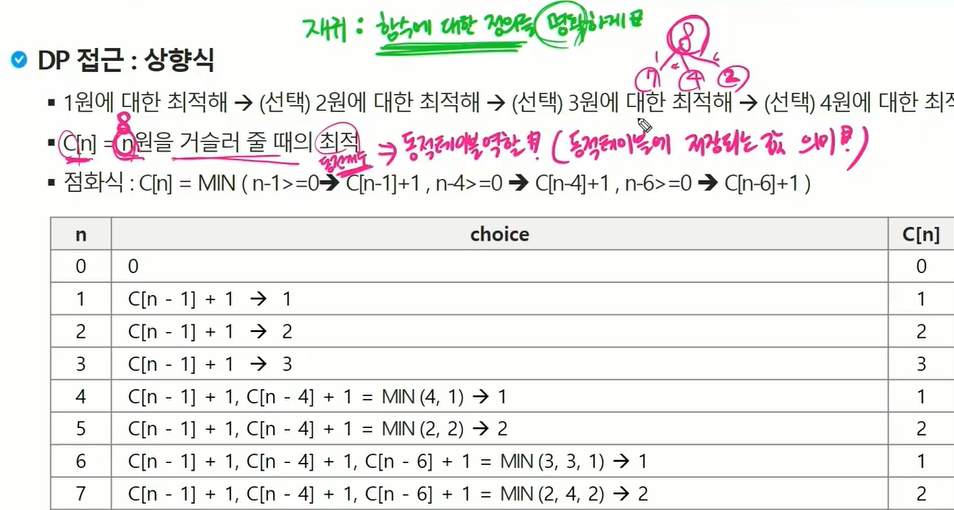
동전 거스름 돈 구하기

***** 재귀: 함수에 대한 정의를 명확하게!

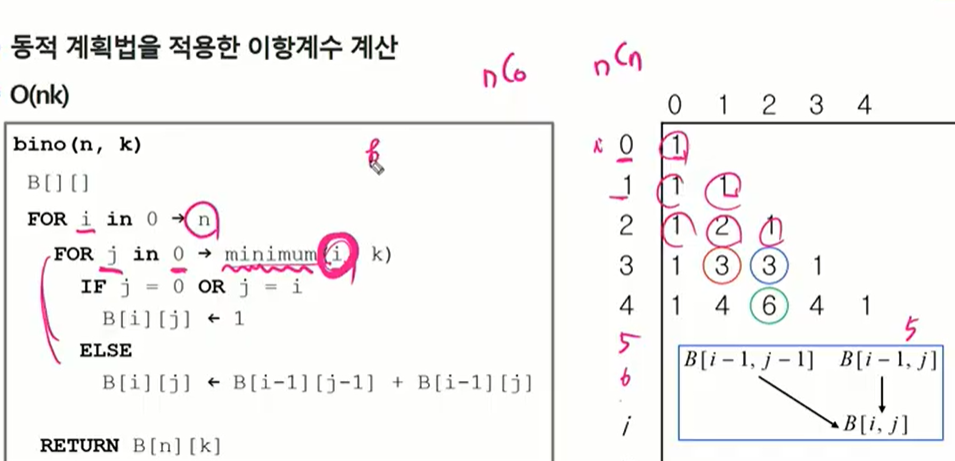
이항계수

파스칼의 삼각형

DP는 최종적으로 구해야되는 문장 써보자