[Algorithm] Algorithm 다익스트라
최단경로
최단경로 정의
- 간선의 가중치가 있는 그래프에서 두 정점 사이의 경로들 중에 간선의 가중치의 합이 최소인 경로.
하나의 시작정점에서 끝 정점까지의 최단경로.
- 다익스트라 알고리즘 -> 음의 가중치를 허용하지 않음
벨만 포드 알고리즘 -> 음의 가중치 허용
- 모든 정점에 대한 최단경로 -> 플로이드 와셜 알고리즘.
아직 고려되지 않은 정점 중 시작점에서 자신에게 오는 가장 가까운 애를 먼저 찾음. 처리되지 않은 애들 중.
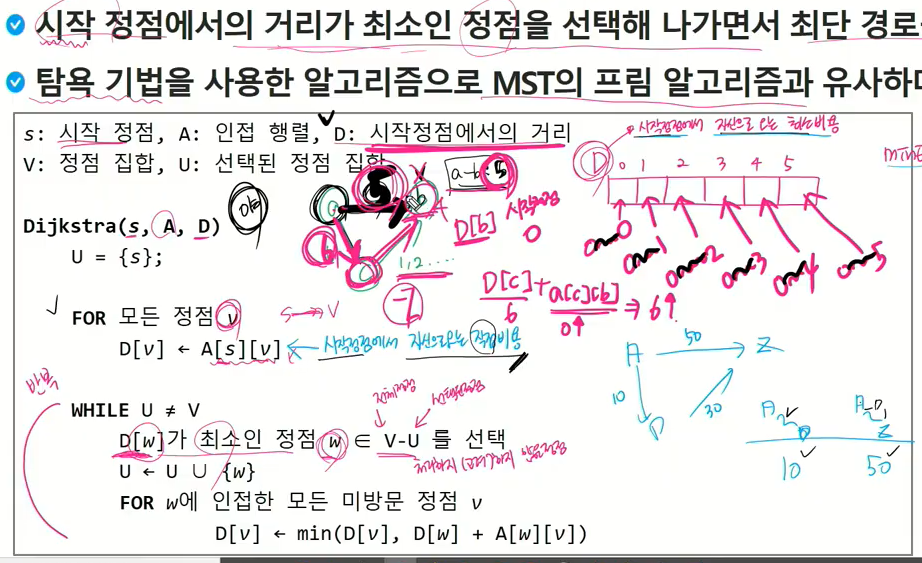
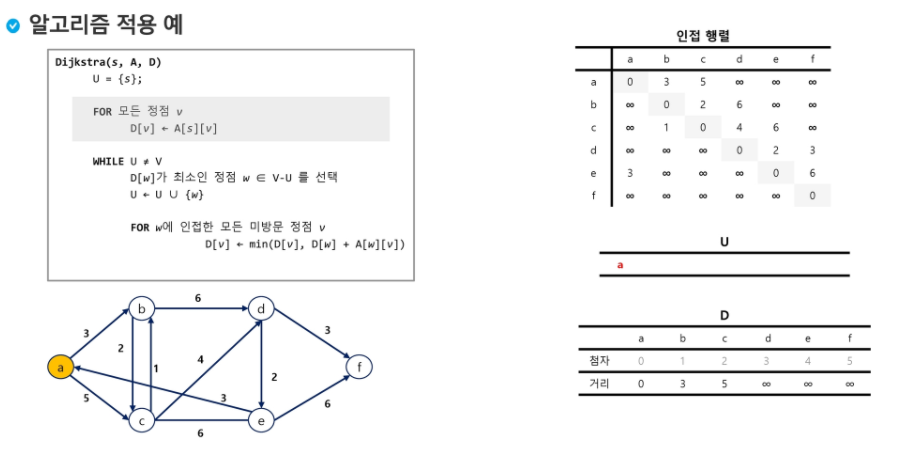
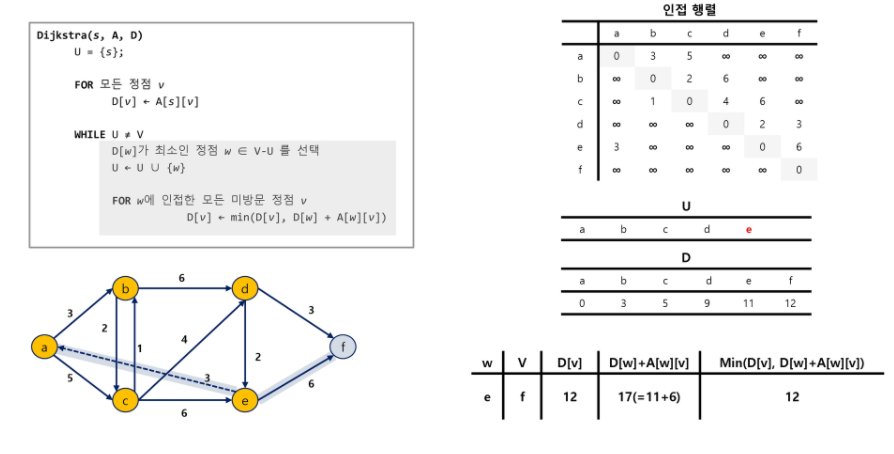
다익스트라 알고리즘
-시작 정점에서의 거리가 최소인 정점을 선택해 나가면서 최단 경로를 구하는 방식.
- 탐욕기법을 사용한 알고리즘으로 MST의 프림 알고리즘과 유사.
선택이 안 된 것 중 하나 선택.
w를 u에 합침.
d[v]는 아직 방문 안한 v에 대해 얘기하는데 이 둘중 어느게 더 작은가.
–
1과 0 중 연결된 애들중 제일 작은 값.
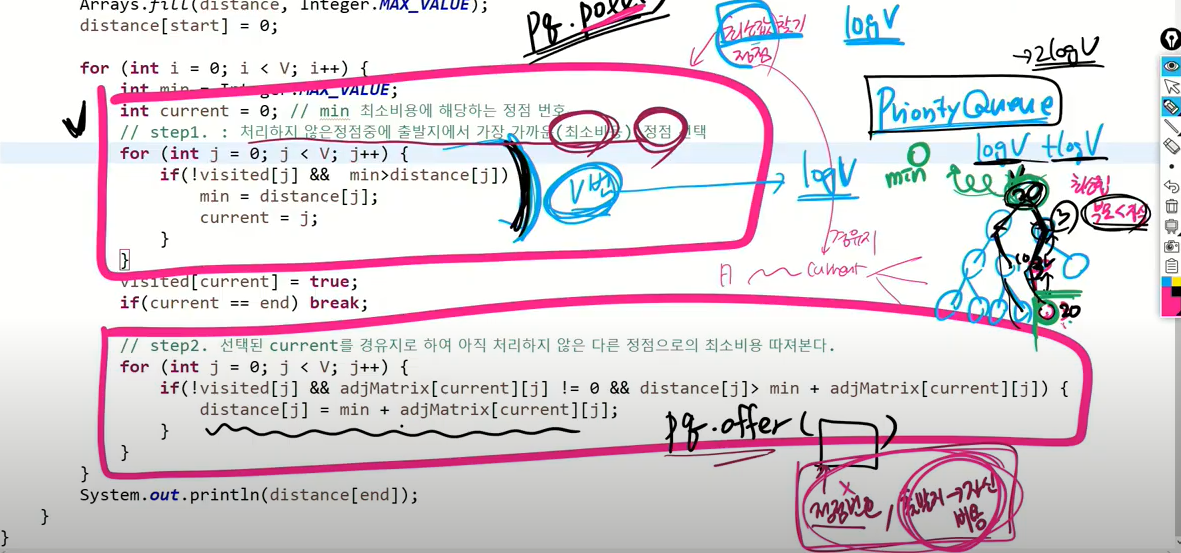
!visited[j] : 아직 선택하지 않은 곳 / adjMatrix[current][j] != 0 : 자기자신으로 가는 경우가 아닐 때 / distance[j] > min + adjMatrix[current][j] : 최소비용과 현재 값의 값이 더 최적이라면 이라고 이해했습니다!!!
인접한 경우에만 가중치 값이 존재하니까 꼭 필요한 것 같아요!
adjMatrix[current][j] != 0 : 자기자신으로 가는 경우가 아닐 때 ==> 자기 자신보다는 연결이 되어 있는 경우만 이 더 좋아 보이내요
인접행렬이여서 자기 자신인 0을 확인했고 인접리스트로 구현한다면 확인하지 않고도 코드 작성할 수 있어요
왜 pq를 쓰는지 아는게 중요하다 최소값 정점 빠르게 찾기 위해 o(1)만에 꺼내는 느낌으로 코드 짠다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Dijkstra {
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int V = Integer.parseInt(br.readLine());
int start = 0; //출발점
int end = V-1; //도착점.
int [][] adjMatrix = new int[V][V];//인접행렬
StringTokenizer st = null;
for(int i =0; i<V;i++) {
st = new StringTokenizer(br.readLine()," ");
for(int j =0; j<V;j++) {
adjMatrix[i][j] = Integer.parseInt(st.nextToken());
}
}
int [] distance = new int[V];
boolean [] visited = new boolean[V];
Arrays.fill(distance, Integer.MAX_VALUE);
distance[start] = 0;
for(int i =0; i<V;i++) {
//step1. 처리하지 않은 정점 중 출발지에 가장 가까운 정점 선택
int min = Integer.MAX_VALUE;
int current=0; //min의 최소비용에 해당하는 정점번호.
for(int j =0; j<V; j++) {
if(!visited[j] && min > distance[j]) {
// distance의 값 중 최소의 값을 찾아야 하니까.
min = distance[j];
current = j;
}
}
visited[current] = true;
if(current== end)break; //끝이면 다른곳으로 경유해서 거쳐서 가는 애를 찾을 필요 없다.
//출발지에서 목적지 가는 모든 경우 비교할 거아니면 여기서 끝내도 된다.
//step2. 선택된 current를 경유지로 하여 아직 처리하지 않은 다른 정점으로 최소비용을 따져본다.
for(int j =0; j<V;j++) {
if(!visited[j] && adjMatrix[current][j]!=0 && distance[j]>min+adjMatrix[current][j]) {
//출발지에서 current까지 더한게 최소비용 . 출발지에서 j로 오는 비용보다 크면 원래 거보다 거쳐서 오는게 더 유용하다는 의미니까
distance[j] = min+adjMatrix[current][j];
}
}
}
System.out.println(distance[end]);
//만약 출발지에서 어떤 경유로 가도 end 못가면 max_value
//그래서 초기값인 maxvalue면 어떤 식으로 해도 목적지에 못간다.
}
}
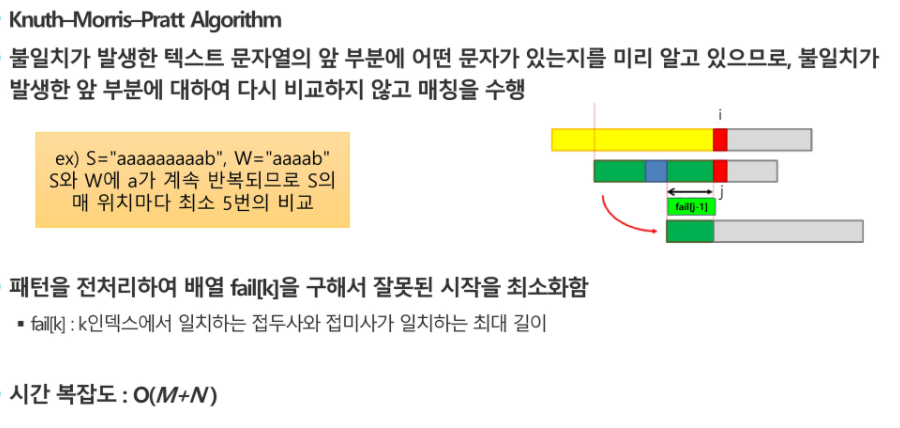
KMP 알고리즘도 Knuth-Morris-Pratt Algorithm
불일치가 발생한 텍스트 문자열의 앞 부분에 어떤 문자가 있는지 미리 알고 있으므로 불일치가 발생한 앞 부분에 대해 다시 비교하지 않고 매칭을 수행.
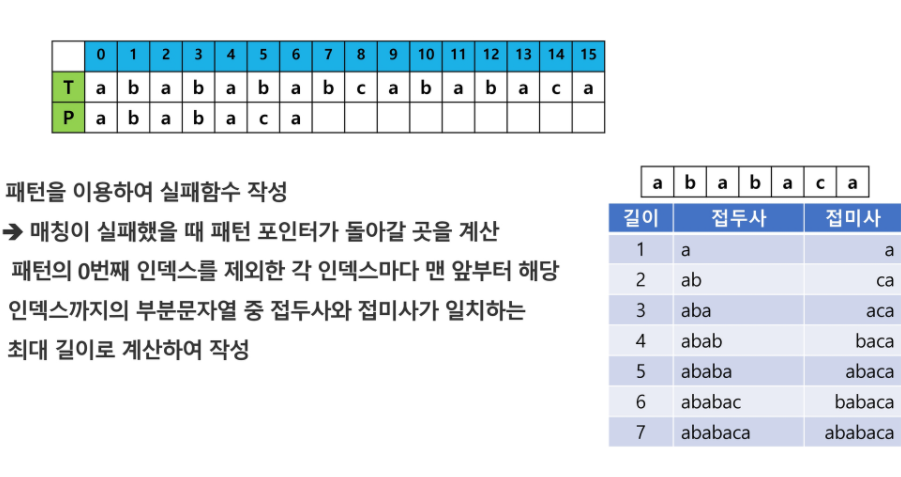
패턴을 전처리 해 배열 fail[k]를 구해 잘못된 시작을 최소화함. -> fail[k]: k인덱스에서 일치하는 접두사와 접미사가 일치하는 최대 길이. 시간 복잡도 : O(M+N);
ex)

패턴 매칭에 사용되는 알고리즘
- 고지식한 패턴 검색 알고리즘(브루트포스)
- 라빈 - 카프 알고리즘
- 보이어- 무어 알고리즘
- kmp 알고리즘.
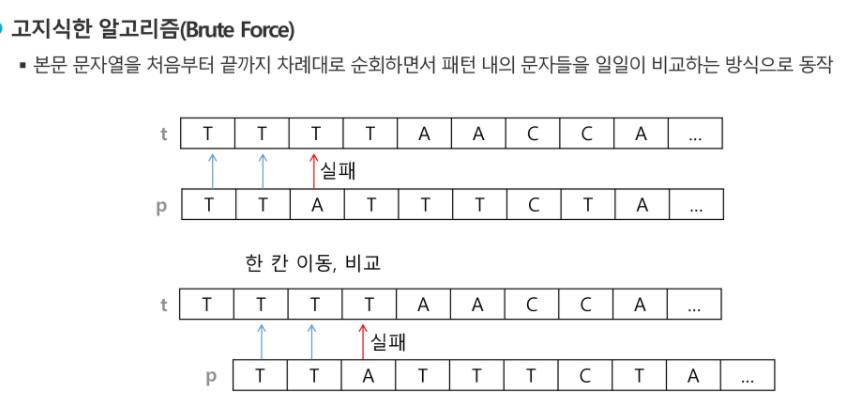
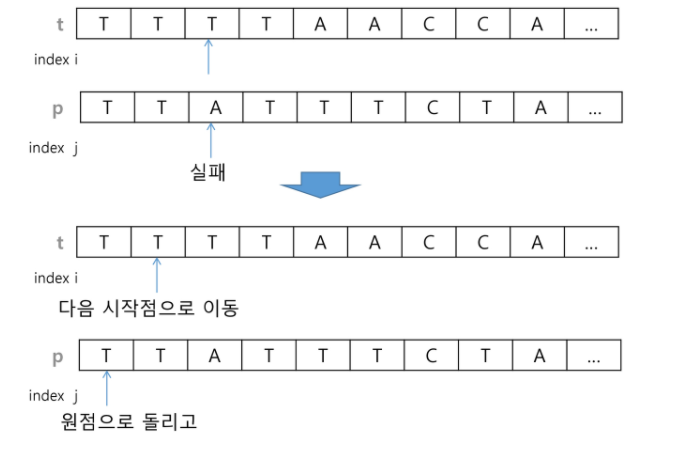
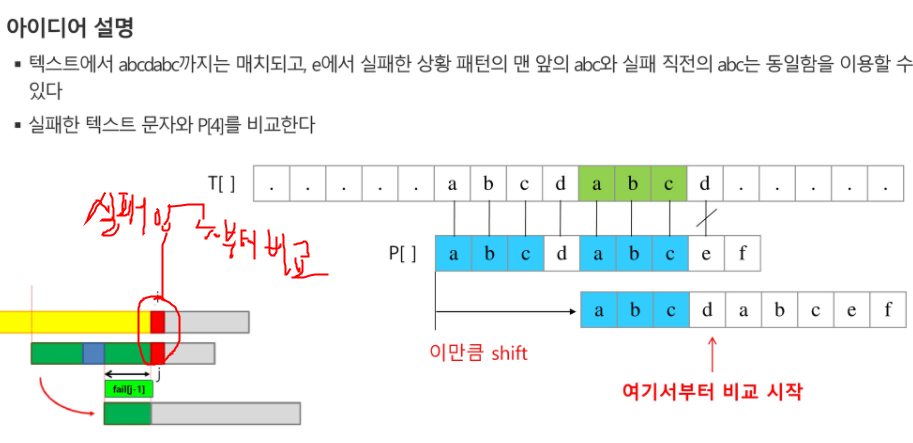
kmp는 틀린 부분 발생했을 떄 거기서 부터 앞은 맞은 부분을 두고 틀린부분 부터 이 정보로 맨앞으로 돌아가는게 아니라 틀린애 대신에 밀어서 그 자리에서 최대한 비교. 안되면 다음으로 감.
fail이라 적어놨는데(실패함수) 사실 함수가 아니라 문자열의 비교에 실패했을 시 이 패턴포인터가 어느위치로 가야하는지 알려줘야하는 길잡이 배열.
KMP 알고리즘