[Algorithm] Algorithm 그래프
선형 : 1:1 , 한줄로 줄 세울 수 있다 비 선형: 1:1이 아닌 관계(1:다, 다대다) -> 트리, 그래프
그래프는 아이템(사물 또는 추상적 개념)들과 이들의 연결 관계를 표현
- 정점(Vertex): 그래프의 구성요소로 하나의 연결점.
- 간선(Edge): 두 정점을 연결하는 선
- 차수(degree): 정점에 연결된 간선의 수
- 그래프는 정점(Vertex)들의 집합과 이들을 연결하는 간선(Edge)들의 집합으로 구성된 자료구조
V: 정점의 개수, E: 그래프에 포함된 간선의 개수 V개의 정점을 가지는 그래프는 최대 V(V-1)/2간선이 가능 예) 5개 정점이 있는 그래프의 최대 간선수는 10(=>54/2)개이다
- 선형 자료구조나 트리 자료구조로 표현하기 어려운 N:N관계를 가지는 원소들 표현하기 용이.
#### 그래프 유형
- 무향 그래프(방향성 無) => 양방향 관계
- 유향 그래프
- 가중치 그래프
- 사이클 없는 방향 그래프( DAG, Directed Acyclic Graph)
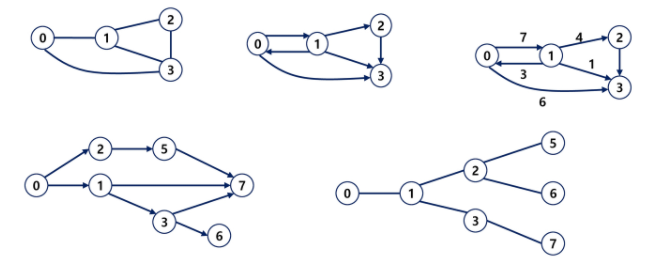
- 완전 그래프 : 정점들에 대해 가능한 모든 간선을 가진 그래프
- 부분 그래프 : 원래 그래프에서 일부 정점이나 간선을 제외한 그그래프
- 트리는 싸이클이 없는 무향 연결 그래프이다.
- 두 노드 사이에는 유일한 경로가 존재한다.
- 각 노드는 최대 하나의 부모 노드가 존재할 수 있다.
- 각 노드는 자식 노드가 없거나 하나 이상이 존재할 수 있다.
인접 정점
인접(Adjacency)
- 두 개의 정점이 간선에 존재(연결됨)하면 서로 인접해 있다고 한다.
- 완전 그래프에 속한 임의의 두 정점은 모두 인접해 있다.
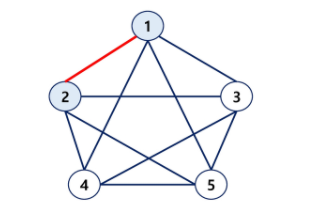
그래프 경로
경로란(path) 어떤 정점에서 시작해 다른 정점(B)로 끝나는 순회로 두 정점 사이를 잇는 간선들을 순서대로 나열한 것.
완전탐색하면 루트부터 하는데 그래프는 그런게 없으니까 임의의 정점에서 구해도 다 탐색이 가능하다.(임의의 정점이 다른 하나의 정점에 연결되어 있으면 다 탐색 가능)
- 0~6의 경로
- 정점들: 0-2-4-6
간선들: (0,2),(2,4),(4,6)
- 경로 중 한 정점을 최대 한 번만 지나는 경로를 단순경로라 한다.
- 0-2-4-6, 0-1-6
순환 경로(Cyclic Path)
- 경로의 시작점과 끝 점이 같은
- 경로에서 어떤 정점을 2번 이상 거치는 경우
- 1-3-5-1
그래프 표현
간선의 정보를 저장하는 방식, 메모리나 성능을 고려해서 결정
인접행렬(Adjacent matrix) 1.VxV 크기의 2차원 배열을 이용해 간선 정보를 저장 2.배열의 배열(Reference Array)
인접 리스트(Adjacent List) 각 정점마다 다른 정점으로 나가는 간선의 정보를 저장
간선 리스트(Edge List) 간선(시작 정점, 끝 정점)의 정보를 객체로 표현하여 리스트에 저장
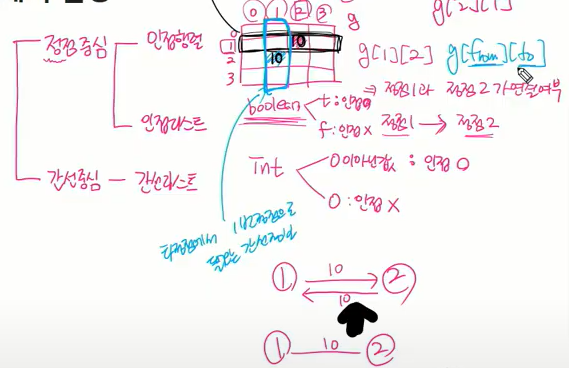
두 정점을 연결하는 간선의 유무를 행렬로 표현
- VxV 정방 행렬
- 행 번호와 열 번호는 정점에 대응
두 정점이 인접되어 있으면 1 , 아니면 0으로 표현
무향 그래프 i번쨰 항 = i번쨰 열의 합 = Vi의 차수
- 유향 그래프 행 i의 합 = Vi의 진출 차수 열 i의 합 = Vi의 진입 차수.
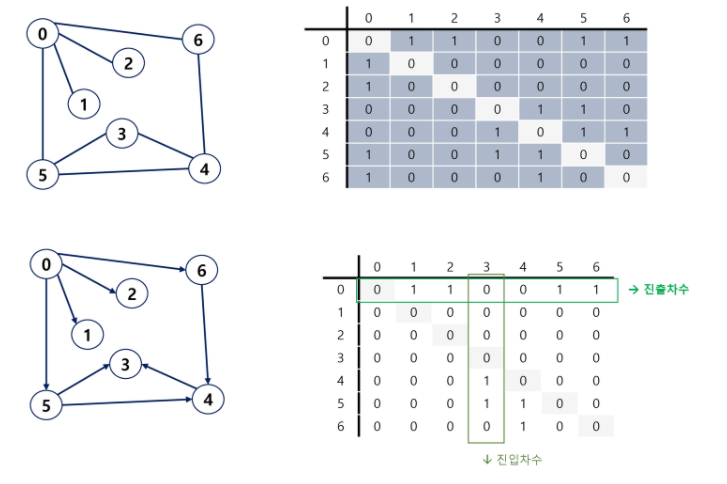
인접 행렬의 단점은?
희소 그래프(sparse Graph) vs 밀집 그래프 (Dense Graph)
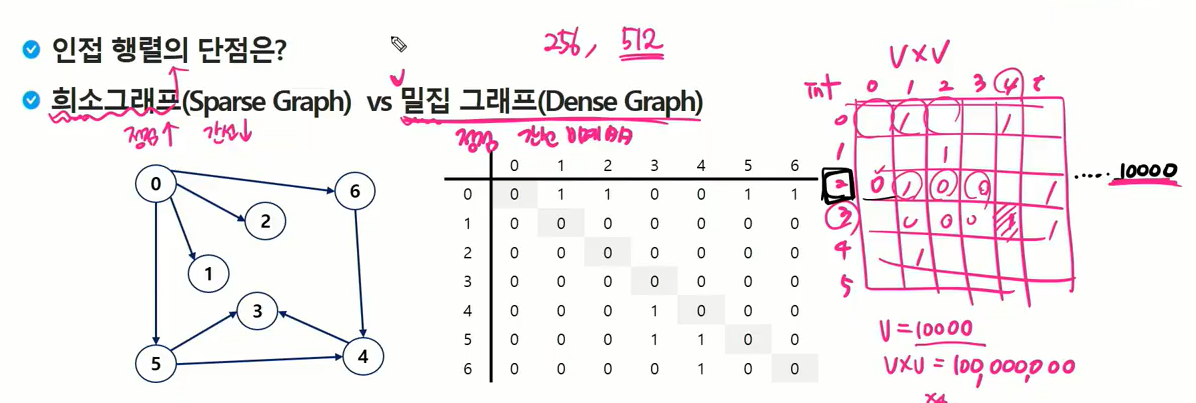
희소 그래프일때는 인접 리스트를 쓰다.
인접 리스트를
각 정점에 대한 인접 정점들을 순차적으로 표현
하나의 정점에 대한 인접 정점들을 각각 노드로 하는 연결리스트로 저장.
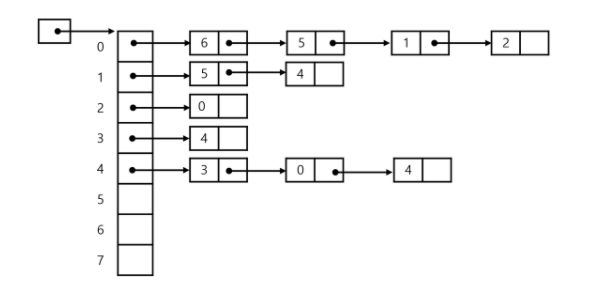
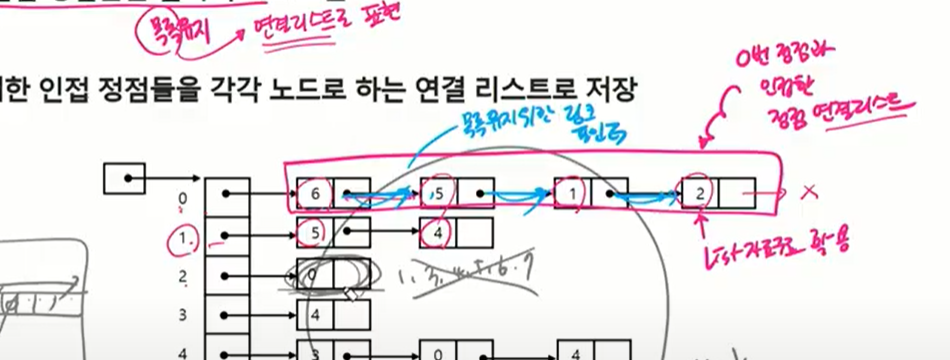
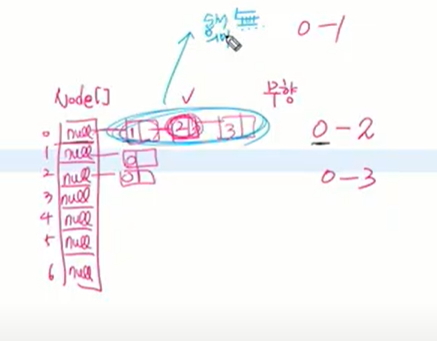
맨 앞 배열들처럼 있는게 from 거기서 오른쪽으로 나온 애들을 to로 보면 된다.
0번 정점 기준으로 인접한 애들 1번 정점 기준으로 인접한 애들.. … 그렇게 옆으로 정점이 이어져있다.
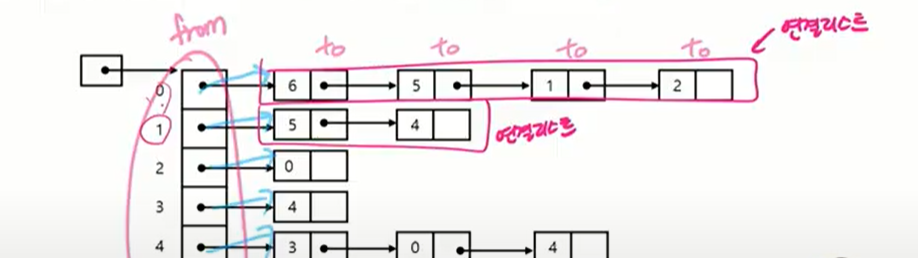
연결리스트의 head를 가지고 있으면(첫번째) 다 가지고 있는 거. 연결리스트 만들 때 정점 개수만큼 만들고 자신의 연결리스트의 head만 유지한다.
근데 연결리스트 못 만들겠다고 어레이리스트로 만들면 어레이리스트로 저장하면 된다.
구현 방식에 따라 틀리다.
연결리스트로 만들고 하나하나 노드로 만들면 Node타입의 배열로 선언하면 됨.
만약 연결리스트로 안 만들고 ArrayList로 만들면 그 어레이리스트로 담는 배열. 그럼 얘는 ArrayList의 배열이 된다. (2번이 더 쉽다고 생각할 수 있는데 어레이 리스트는 자바의 컬렉션이고 컬렉션은 성능상 불리함이 좀 있다.) 직접 연결 리스트로 구현하는게 더 좋다.(30프로 이상 속도 개선)
그리고 연결 리스트 안의 순서는 중요한가? 전혀 중요하지 않다. 앞으로 삽입하는 알고리즘으로 추가하면 됨.(head가 가리키는 거 계속 바꿔주니까 복잡할 게 전혀 없다.)
(2차원 배열로 만드는 거보다 손이 더 가서 잘 안쓰려고 하는데 알아두는게 좋다.)
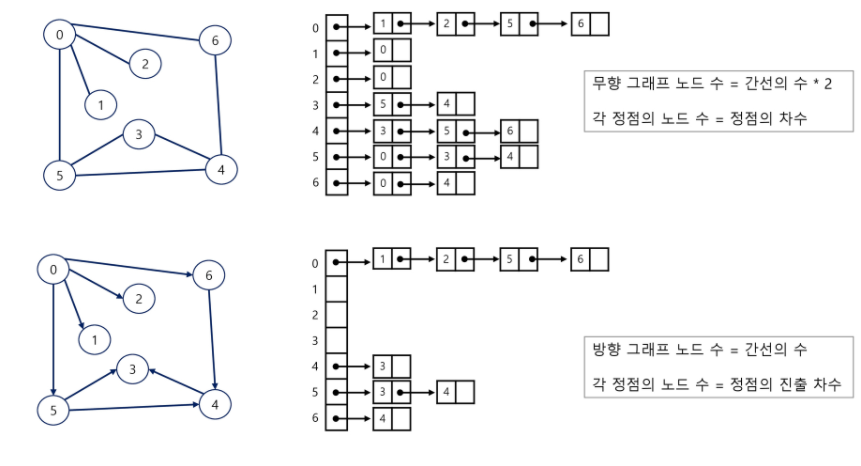
위는 무향인데 0-6, 6-0 추가 간선 8개인데 의미로는 16개. 즉 4,1,1,2,3,3,2개로 16개.(대칭되게 인접행렬 만든거 처럼 인접행렬 만들 때도 뒤집어서 관계성 표현 똑같이 해줘야 한다.)
근데 밑은 유향이니까 그럴 필요가 없다. 유향그래프가 0-6의 그래프는 0번에서만 하면 되지 6번 인접헤드에서 할 필요도 없다.
따라가면서 자신하고 연결된 애의 수가 된다.
간선 리스트
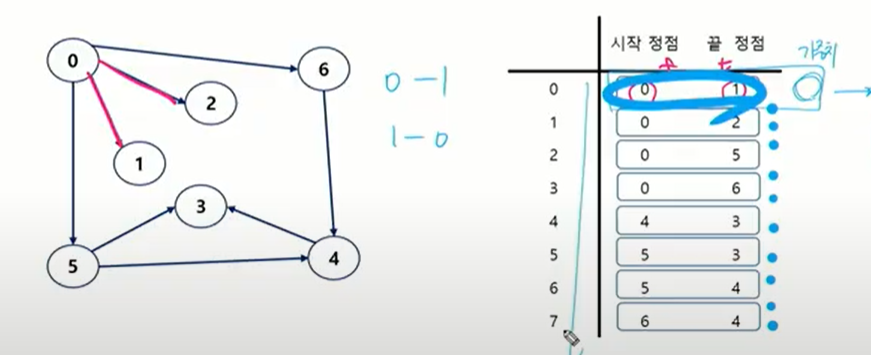
- 두 정점에 대한 간선 그 자체를 객체로 표현하여 리스트로 저장
- 간선을 표현하는 두 정점의 정보를 나타냄(시작 정점, 끝 정점)
어느 정점에서 어느정점으로 가는 간선정보고 그때 가중치가 얼마인지.
무향이면 간선정보 하나 더 만들어서넣어주면 됨.
그래프 탐색(순회)
그래프 순회는 비 선형 구조인 그래프로 표현된 모든 자료(정점)를 빠짐 없이 탐색하는 것을 의미한다
두가지 방법
- 너비 우선 탐색(Breadth frist search, BFS)
- 깊이 우선 탐색(descriptionth frist search, DFS)
BFS(Breadth First Search)
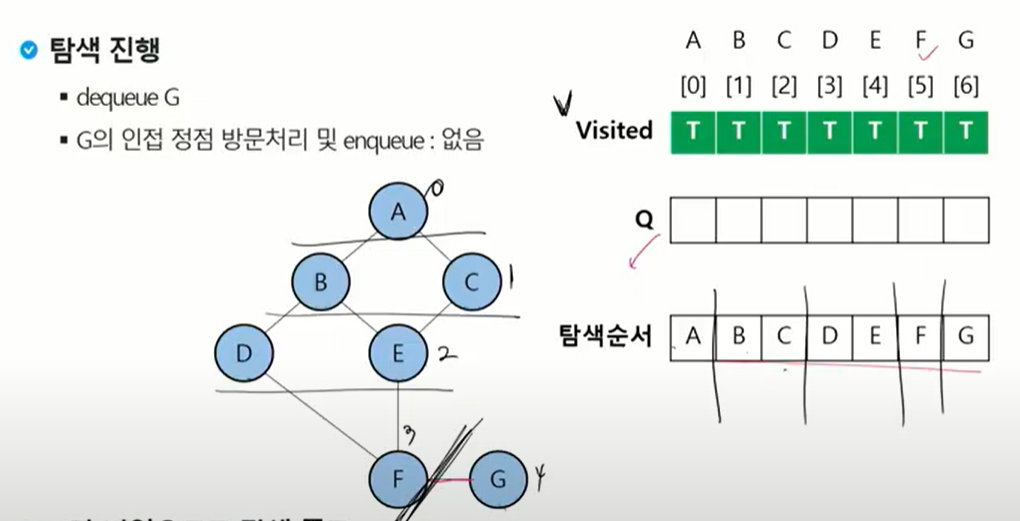
너비 우선 탐색은 탐색 시작점의 인접한 정점들을 먼저 모두 차례로 방문한 후에, 방문했던 정점을 시작점으로 해서 다시 이넞ㅂ한 정점들을 차례로 방문하는 방식
인접한 정점들에 대해 탐색 한 후, 차례로 다시 너비우선 탐색을 진행해야 하므로, 선입 선출 형태의 자료구조인 큐를 활용함.
최단 거리 찾을 때 BFS 많이 사용.

package com.ssafy.graph;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
/*
7
8
0 1
0 2
1 3
1 4
2 4
3 5
4 5
5 6
*/
public class G1_AdjMatrixTest {
static int N;
static boolean[][] adjMatrix;
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
int C = Integer.parseInt(br.readLine());
adjMatrix = new boolean[N][N];
StringTokenizer st = null;
for(int i =0; i<C;i++) {
st = new StringTokenizer(br.readLine()," ");
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
adjMatrix[to][from] = adjMatrix[from][to] =true;
}
bfs();
}
private static void bfs() {
Queue<Integer> queue = new LinkedList<Integer>();
boolean [] visited = new boolean[N];
//탐색 시작 정점 : 0으로 출발
int start =0;
queue.offer(start);
visited[start] = true;
while(!queue.isEmpty()) {
int current = queue.poll();
//현재 정점에 관련된 처리
System.out.println((char)(current+65));
//인접 정점 탐색
for(int i = 0;i<N;i++) {
if(adjMatrix[current][i] //인접정렬
&& !visited[i]) {//미방문 정점
queue.offer(i);
visited[i] = true;
}
}
}
}
}
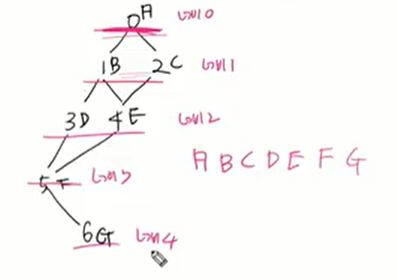
0번 노드에서 마지막 노드 따라간 다음 그 마지막 노드 뒤에 붙여야(0-2면) 0-3이면 똑같이 2 마지막 따라가서 붙인다. 그리고 이 부분들이 상관이 없다.
그리고 연결리스트는 방향이 상관 없다.(순서 아무 상관 없음)
연결리스트 맨뒤 넣으려면 맨뒤 찾는 작업해야됨 근데 맨 앞에 집어넣는 알고리즘도 배웠다.
없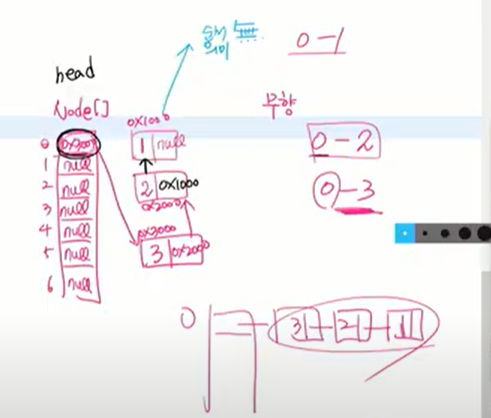 즉 연결리스트는 지금 구현됨.(순서 아무 상관 없음) 즉 뒤로 넣을 필요 굳이 없고 앞(첫번째)으로 집어 넣어도 상관없음.
즉 연결리스트는 지금 구현됨.(순서 아무 상관 없음) 즉 뒤로 넣을 필요 굳이 없고 앞(첫번째)으로 집어 넣어도 상관없음.
0번 정점에서 아무것도 들어있지 않은 null이 고스란이 넘어감. 그렇게 만들어진 객체의 레퍼런스를 from 의 인접리스트에 집어넣음.
adjList[from] = new Node(to,adjList[from]);
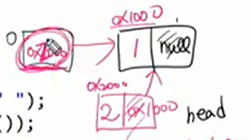
from 의 정점의 헤드를 지금 새로 만드는 애로 바꿔라 대신 새로 만드는 애가 첫째가 되기 위해선 기존 헤드 정보를 넥스트에 두어서 자신의 뒤로 오게 하면 계속 첫번쨰 노드로 집어넣게 되는 것
이렇게 만드는 법을 꼭 알아둬야한다(쉬운거만 할 수 없다.)
temp가 각 이동하게(tmep가 바라보는 next)
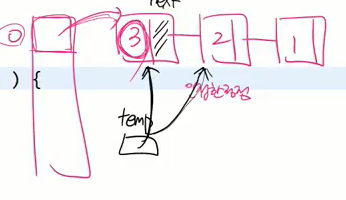
for(Node temp = adjList[current]; temp!=null; temp = temp.next)
이 부분은 인접 정점만 반복처리 탐색하는 법이 바뀌는 거 bfs 논리는 그대로임. 이 아래는 인접 체크 조건이 바뀐거.
정점이 1000개인데 한 정점마다 간선정보가 2,3개 미만이면 원래 인접행렬은 인접행렬 계속 찾았다면 인접리스트는 인접한 애들만 처리해서 처리도 줄어들고 공간적으로 관계 없는 애들까지 자리 차지하는게 아니라 있는 애들만 쓰기 때문에 공간 효율도 좋다.
-> 인접리스트가 훨씬 좋다.
근데 출력이 약간 다른데 위의 리스트는 앞에 노드를 계속 넣어서 그럼(뒤가 아니라)
즉 바뀐 부분은 너비가 같은 부분들임.
인접행렬에서 무조건 오른쪽으로 탐색한다고 맞나? 왼쪽방향으로 탐색해도 동일함.
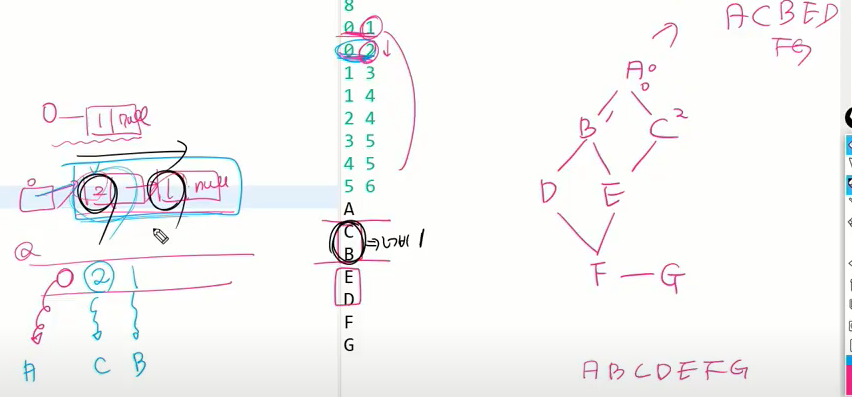
너비가 같은 거 안에서는 순서는 상관이 없다.
이렇게 안하려면 마지막 노드로 매번 집어넣어야됨. 근데 순서가 막 바뀌어 들어올수도. 결과가 이렇게 들어오는 이유 아려면 인접리스트가 어떻게 들어오는지 꼭 이해해야된다.
먼저 처리한 인접리스트 정점이 맨 뒤, 마지막 처리한 인접리스트 정점이 맨 앞이라 순서가 바뀐거 처럼 느끼졈.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
/*
7
8
0 1
0 2
1 3
1 4
2 4
3 5
4 5
5 6
*/
public class G2_AdjListTest {
static class Node{
int vertex;
Node next;
//연결리스트의 요소 하나하나 나타내려 만듬.
//정점 번호랑 연결리스트 역할위한 링크의노드 포인터 가짐.
public Node(int vertex, Node next) { //생성자 생성.(노드생성)
super();
this.vertex = vertex;
this.next = next;
}
public Node(int vertex) { //정점정보만 있는 노드 생성.
super();
this.vertex = vertex;
}
@Override
public String toString() { //오버라이딩
return "Node [vertex=" + vertex + ", next=" + next + "]";
}
}
static int N;
static Node[] adjList; //노드 배열
//0번 정점에 서 인접해있는 인접 정점들의 연결리스트의 몫(head)
//기차의 처음만 가져오면 다 딸려오듯. 리스트 처음만 알면 링크 따라 다 끌고 옴.
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
int C = Integer.parseInt(br.readLine());
adjList = new Node[N]; //정점의 개수만큼 배열 만듬
StringTokenizer st = null;
for(int i =0; i<C;i++) {
st = new StringTokenizer(br.readLine()," ");
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
adjList[from] = new Node(to,adjList[from]);
//0번 노드에서 마지막 노드 따라간 다음 그 마지막 노드 뒤에 붙여야(0-2면)
//0-3이면 똑같이 2 마지막 따라가서 붙인다.
//그리고 이 부분들이 상관이 없다.
//from 의 정점의 헤드를 지금 새로 만드는 애로 바꿔라 대신 새로 만드는 애가 첫째가 되기 위해선 기존 헤드 정보를 넥스트에 두어서 자신의 뒤로 오게 하면 계속 첫번쨰 노드로 집어넣게 되는 것
adjList[to] = new Node(from,adjList[to]); //뒤집어서 한번 더해야
//이렇게 하면 인접리스트 끝. 간선개수만큼 하면 지금 한 작업들이 계속 반복되면 각 노드마다 인접한 정점으로 연결리스트 만들고 각 헤드를 다 물고 있게 된다.
}
bfs();
}
private static void bfs() {
Queue<Integer> queue = new LinkedList<Integer>();
boolean [] visited = new boolean[N];
//탐색 시작 정점 : 0으로 출발
int start =0;
queue.offer(start);
visited[start] = true;
while(!queue.isEmpty()) { //큐가 비어있지 않을때까지 돌면서
int current = queue.poll(); //뺀다(가장 앞의 정점)
//현재 정점에 관련된 처리
System.out.println((char)(current+65));
//인접 정점 탐색(여기서 부터 달라짐)
//아까는 인접행렬이라 정점개수만큼 들여다보며 하나씩 체크했는데 이번은 인접리스트라 어떤정점의 인접리스트엔 인접한 애들만 들어있ㅅ다.
// 그래서 인접여부 체크 할 필요가 없다.
for(Node temp = adjList[current]; temp!=null; temp = temp.next) {
//Node temp = adjList[current]; 이게 인접리스트의 첫번쨰 해드
//for(Node temp = adjList[current]; temp!=null; temp = temp.next) { 이 부분은 인접 정점만 반복처리
//탐색하는 법이 바뀌는 거 bfs 논리는 그대로임. 이 아래는 인접 체크 조건이 바뀐거. 불필요한 조건이 없어짐.
if(!visited[temp.vertex]) { //연결은 되어있으니 인접여부는 판단할 필요가 없고 노드가 저장된 정점을 보면 그게 어떤 정점 정보인지 알 수 있다. 그게 방문되었는지 아닌지만 체크
queue.offer(temp.vertex);
visited[temp.vertex] = true;
}
}
}
}
}
꼭 기억해야 상황따라 인접행렬 못 만드는 경우가 있다! 그럼 인접리스트 만들어야 된다.
굳이 못 만들겠다면 어레이리스를 차곡차곡 해서 여러개 만들수 있긴 한데 아무튼 인접리스트 부분은 꼭 알아두자.
DFS 알고리즘
시작정점의 한 방향으로 갈 수 있는 경로 있는 곳 까 깊이탐색해가다가 더 이상 갈 곳이 없게 되면 가장 마지막에 만났던 갈림길 간선이 있는 정점으로 되돌아와서 다른 방향의 정점으로 계속 탐색을 반복하여 결국 모든 정점을 방문하는 순회방법.
가장 마지막에 만났던 갈림길의 정점으로 되돌아가서 다시 깊이우선탐색을 반복해야 하므로 재귀적으로 구현하거나 후입선출 구조의 스택사용.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
/*
7
8
0 1
0 2
1 3
1 4
2 4
3 5
4 5
5 6
*/
public class G2_AdjListTest {
static class Node{
int vertex;
Node next;
//연결리스트의 요소 하나하나 나타내려 만듬.
//정점 번호랑 연결리스트 역할위한 링크의노드 포인터 가짐.
public Node(int vertex, Node next) { //생성자 생성.(노드생성)
super();
this.vertex = vertex;
this.next = next;
}
public Node(int vertex) { //정점정보만 있는 노드 생성.
super();
this.vertex = vertex;
}
@Override
public String toString() { //오버라이딩
return "Node [vertex=" + vertex + ", next=" + next + "]";
}
}
static int N;
static Node[] adjList; //노드 배열
static boolean[] visited;
//0번 정점에 서 인접해있는 인접 정점들의 연결리스트의 몫(head)
//기차의 처음만 가져오면 다 딸려오듯. 리스트 처음만 알면 링크 따라 다 끌고 옴.
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
int C = Integer.parseInt(br.readLine());
adjList = new Node[N]; //정점의 개수만큼 배열 만듬
StringTokenizer st = null;
for(int i =0; i<C;i++) {
st = new StringTokenizer(br.readLine()," ");
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
adjList[from] = new Node(to,adjList[from]);
//0번 노드에서 마지막 노드 따라간 다음 그 마지막 노드 뒤에 붙여야(0-2면)
//0-3이면 똑같이 2 마지막 따라가서 붙인다.
//그리고 이 부분들이 상관이 없다.
//from 의 정점의 헤드를 지금 새로 만드는 애로 바꿔라 대신 새로 만드는 애가 첫째가 되기 위해선 기존 헤드 정보를 넥스트에 두어서 자신의 뒤로 오게 하면 계속 첫번쨰 노드로 집어넣게 되는 것
adjList[to] = new Node(from,adjList[to]); //뒤집어서 한번 더해야
//이렇게 하면 인접리스트 끝. 간선개수만큼 하면 지금 한 작업들이 계속 반복되면 각 노드마다 인접한 정점으로 연결리스트 만들고 각 헤드를 다 물고 있게 된다.
}
bfs();
visited = new boolean[N];
visited[0] = true;
dfs(0);
}
private static void bfs() {
Queue<Integer> queue = new LinkedList<Integer>();
boolean [] visited = new boolean[N];
//탐색 시작 정점 : 0으로 출발
int start =0;
queue.offer(start);
visited[start] = true;
while(!queue.isEmpty()) { //큐가 비어있지 않을때까지 돌면서
int current = queue.poll(); //뺀다(가장 앞의 정점)
//현재 정점에 관련된 처리
System.out.println((char)(current+65));
//인접 정점 탐색(여기서 부터 달라짐)
//아까는 인접행렬이라 정점개수만큼 들여다보며 하나씩 체크했는데 이번은 인접리스트라 어떤정점의 인접리스트엔 인접한 애들만 들어있ㅅ다.
// 그래서 인접여부 체크 할 필요가 없다.
for(Node temp = adjList[current]; temp!=null; temp = temp.next) {
//Node temp = adjList[current]; 이게 인접리스트의 첫번쨰 해드
//for(Node temp = adjList[current]; temp!=null; temp = temp.next) { 이 부분은 인접 정점만 반복처리
//탐색하는 법이 바뀌는 거 bfs 논리는 그대로임. 이 아래는 인접 체크 조건이 바뀐거. 불필요한 조건이 없어짐.
if(!visited[temp.vertex]) { //연결은 되어있으니 인접여부는 판단할 필요가 없고 노드가 저장된 정점을 보면 그게 어떤 정점 정보인지 알 수 있다. 그게 방문되었는지 아닌지만 체크
queue.offer(temp.vertex);
visited[temp.vertex] = true;
}
}
}
}
private static void dfs(int current) { //bfs랑 비슷 큐에서 뽑아내는 정점이 dfs는 재귀는 현재 받아오는 매개변수 정점이 됨.
// visited[current] = true; 아니면 호출받자마자 재귀할거냐.
//어차피 들어갈 때 하나 호출을 받을 떄 하나 차이가 없다. 순서를 기다렸다는게 아니라 visited하고하냐 하고 들어가냐 차이
System.out.println((char)(current+65));
for(Node temp = adjList[current]; temp!= null; temp = temp.next) {
if(!visited[temp.vertex]) {
visited[current] = true; //체크하고 함수(메서드)타러 갈거냐 / 아니면 호출받자마자 재귀할거냐.(위에거)
//혹시나 방ㅁ문체크코드 아까처럼 짜고싶으면 항상 호출하는 코드에 쌍이 되게 넣어주자.
//들어갈떄 하느냐 문 열자마자 차이(사실 차이 없음)
dfs(temp.vertex);
}
}
}
}