[python] python Algorithm
공간 복잡도
- 알고리즘 계산 복잡도는 다음 두 가지 척도로 표현될 수 있음
- 시간 복잡도: 얼마나 빠르게 실행되는지
- 공간 복잡도: 얼마나 많은 저장 공간이 필요한지
좋은 알고리즘은 실행 시간도 짧고, 저장 공간도 적게 쓰는 알고리즘
- 통상 둘 다를 만족시키기는 어려움
- 시간과 공간은 반비례적 경향이 있음
- 최근 대용량 시스템이 보편화되면서, 공간 복잡도보다는 시간 복잡도가 우선
- 그래서! 알고리즘은 시간 복잡도가 중심
공간 복잡도 대략적인 계산은 필요함
- 기존 알고리즘 문제는 예전에 공간 복잡도도 고려되어야할 때 만들어진 경우가 많음
- 그래서 기존 알고리즘 문제에 시간 복잡도뿐만 아니라, 공간 복잡도 제약 사항이 있는 경우가 있음
- 또한, 기존 알고리즘 문제에 영향을 받아서, 면접시에도 공간 복잡도를 묻는 경우도 있음
Complexity:
- expected worst-case time complexity: O(N)
- expected worst-case space complexity: O(N)
현업에서 최근 빅데이터를 다룰 때는 저장 공간을 고려해서 구현을 하는 경우도 있음
1. 공간 복잡도 (Space Complexity)
- 프로그램을 실행 및 완료하는데 필요한 저장공간의 양을 뜻함
- 총 필요 저장 공간
- 고정 공간 (알고리즘과 무관한 공간): 코드 저장 공간, 단순 변수 및 상수
- 가변 공간 (알고리즘 실행과 관련있는 공간): 실행 중 동적으로 필요한 공간
- $ S(P) = c + S_p(n) $
- c: 고정 공간
- $ S_p(n) $: 가변 공간
빅 오 표기법을 생각해볼 때, 고정 공간은 상수이므로 공간 복잡도는 가변 공간예 좌우됨
2. 공간 복잡도 계산
- 공간 복잡도 계산은 알고리즘에서 실제 사용되는 저장 공간을 계산하면 됨
- 이를 빅 오 표기법으로 표현할 수 있으면 됨
예제1
- n! 팩토리얼 구하기
- n! = 1 x 2 x … x n
- n의 값에 상관없이 변수 n, 변수 fac, 변수 index 만 필요함
- 공간 복잡도는 O(1)
공간 복잡도 계산은 실제 알고리즘 실행시 사용되는 저장공간을 계산하면 됨
def factorial(n):
fac = 1
for index in range(2, n + 1):
fac = fac * index
return fac
예제2
- n! 팩토리얼 구하기
- n! = 1 x 2 x … x n
- 재귀함수를 사용하였으므로, n에 따라, 변수 n이 n개가 만들어지게 됨
- factorial 함수를 재귀 함수로 1까지 호출하였을 경우, n부터 1까지 스택에 쌓이게 됨
- 공간 복잡도는 O(n)
def factorial(n):
if n > 1:
return n * factorial(n - 1)
else:
return 1
효과적인 알고리즘을 만드는 방법
- 바로 IDE에 쓰지 마라. 연습장 부터 키고 생각하자.
2. 알고리즘 문제를 읽고 분석한 후에,
3. 간단하게 테스트용으로 매우 간단한 경우부터 복잡한 경우 순서대로 생각해보면서, 연습장과 펜을 이용하여 알고리즘을 생각해본다.
4. 가능한 알고리즘이 보인다면, 구현할 알고리즘을 세부 항목으로 나누고, 문장으로 세부 항목을 나누어서 적어본다.
5. 코드화하기 위해, 데이터 구조 또는 사용할 변수를 정리하고,
6. 각 문장을 코드 레벨로 적는다.
7. 데이터 구조 또는 사용할 변수가 코드에 따라 어떻게 변하는지를 손으로 적으면서, 임의 데이터로 코드가 정상 동작하는지를 연습장과 펜으로 검증한다.
특정 패턴 찾고 가능한 알고리즘이 보이면 함수레벨로 적지 말고 문장단위로 어떤식으로 흘러가나 적는다.
적은 문장단위 구조에 필요한 데이터 구조나 사용할 변수 정리하고 이를 기반으로 풀리는지 펜으로 해본다. 그 경우가 몇가지 경우에서 다 풀리면 코드레벨에서 작성해서 실행해본다.
정렬(Sort)
정렬 (sorting) 이란?
- 정렬 (sorting): 어떤 데이터들이 주어졌을 때 이를 정해진 순서대로 나열하는 것
- 정렬은 프로그램 작성시 빈번하게 필요로 함
- 다양한 알고리즘이 고안되었으며, 알고리즘 학습의 필수
다양한 정렬 알고리즘 이해를 통해, 동일한 문제에 대해 다양한 알고리즘이 고안될 수 있음을 이해하고, 각 알고리즘간 성능 비교를 통해, 알고리즘 성능 분석에 대해서도 이해할 수 있음
버블 정렬 (bubble sort) 란?
- 두 인접한 데이터를 비교해서, 앞에 있는 데이터가 뒤에 있는 데이터보다 크면, 자리를 바꾸는 정렬 알고리즘
맨 뒤부터 정렬이 된다.
직접 눈으로 보면 더 이해가 쉽다: https://visualgo.net/en/sorting

출처: https://en.wikipedia.org/wiki/Bubble_sort
알고리즘 구현
- 특이점 찾아보기
- n개의 리스트가 있는 경우 최대 n-1번의 로직을 적용한다.
- 로직을 1번 적용할 때마다 가장 큰 숫자가 뒤에서부터 1개씩 결정된다.
- 로직이 경우에 따라 일찍 끝날 수도 있다. 따라서 로직을 적용할 때 한 번도 데이터가 교환된 적이 없다면 이미 정렬된 상태이므로 더 이상 로직을 반복 적용할 필요가 없다.
- for num in range(len(data_list)) 반복
- swap = 0 (교환이 되었는지를 확인하는 변수를 두자)
- 반복문 안에서, for index in range(len(data_list) - num - 1) n - 1번 반복해야 하므로
- 반복문안의 반복문 안에서, if data_list[index] > data_list[index + 1] 이면
- data_list[index], data_list[index + 1] = data_list[index + 1], data_list[index]
- swap += 1
- 반복문 안에서, if swap == 0 이면, break 끝
def bubblesort(data):
for index in range(len(data) - 1):
swap = False
for index2 in range(len(data) - index - 1):#여기서 맨 뒤자리가 정렬이 되었으므로 1씩 줄면서 체크한다.
if data[index2] > data[index2 + 1]:#앞의 데이터가 뒤의 데이터보다 크다면
data[index2], data[index2 + 1] = data[index2 + 1], data[index2]#swap해준다.
swap = True
if swap == False:
break
return data
알고리즘 분석
- 반복문이 두 개 O($n^2$)
- 최악의 경우, $\frac { n * (n - 1)}{ 2 }$
- 완전 정렬이 되어 있는 상태라면 최선은 O(n)
선택정렬
선택 정렬 (selection sort) 란?
- 다음과 같은 순서를 반복하며 정렬하는 알고리즘
- 주어진 데이터 중, 최소값을 찾음
- 해당 최소값을 데이터 맨 앞에 위치한 값과 교체함
- 맨 앞의 위치를 뺀 나머지 데이터를 동일한 방법으로 반복함
직접 눈으로 보면 더 이해가 쉽다: https://visualgo.net/en/sorting

출처: https://en.wikipedia.org/wiki/Selection_sort### 1. 선택 정렬 (selection sort) 란?
- 다음과 같은 순서를 반복하며 정렬하는 알고리즘
- 주어진 데이터 중, 최소값을 찾음
- 해당 최소값을 데이터 맨 앞에 위치한 값과 교체함
- 맨 앞의 위치를 뺀 나머지 데이터를 동일한 방법으로 반복함
직접 눈으로 보면 더 이해가 쉽다: https://visualgo.net/en/sorting

출처: https://en.wikipedia.org/wiki/Selection_sort
- 데이터가 두 개 일때
- 예: dataList = [9, 1]
- datalist[0] > data_list[1] 이므로 data_list[0] 값과 data list[1] 값을 교환
- 예: dataList = [9, 1]
- 데이터가 세 개 일때
- 예: data_list = [9, 1, 7]
- 처음 한번 실행하면, 1, 9, 7 이 됨
- 두 번째 실행하면, 1, 7, 9 가 됨
- 예: data_list = [9, 1, 7]
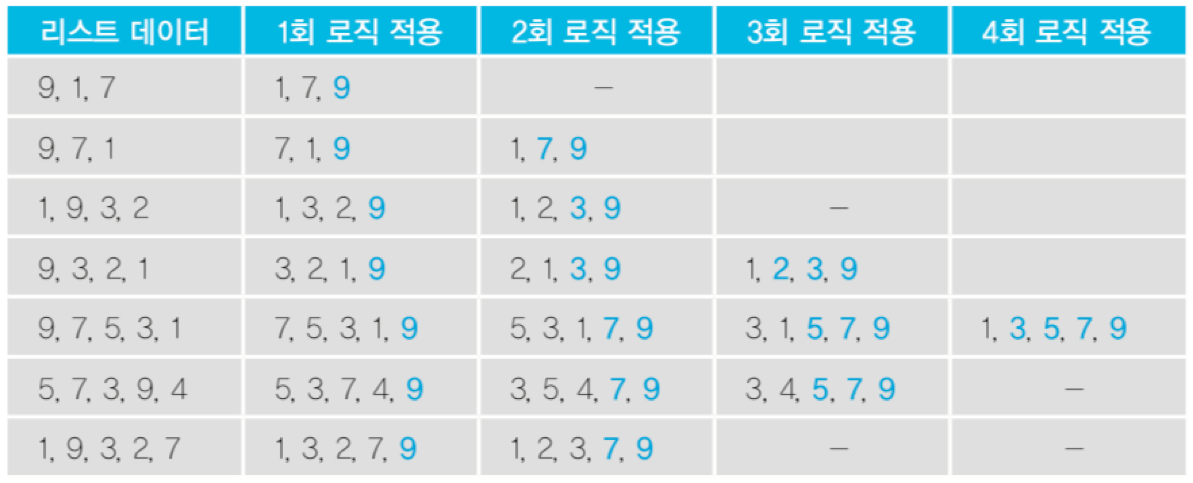
- 데이터가 네 개 일때
- 예: data_list = [9, 3, 2, 1]
- 처음 한번 실행하면, 1, 3, 2, 9 가 됨
- 두 번째 실행하면, 1, 2, 3, 9 가 됨
- 세 번째 실행하면, 변화 없음
- 예: data_list = [9, 3, 2, 1]
알고리즘 구현
- for stand in range(len(data_list) - 1) 로 반복
- lowest = stand 로 놓고,
- for num in range(stand, len(data_list)) stand 이후부터 반복
- 내부 반복문 안에서 data_list[lowest] > data_list[num] 이면,
- lowest = num
- data_list[num], data_list[lowest] = data_list[lowest], data_list[num]
def selection_sort(data):
for stand in range(len(data) - 1):
lowest = stand
for index in range(stand + 1, len(data)): #기준이 되는 점에서 1을 더한값에서 시작하고 데이터 길이만큼 돈다.
if data[lowest] > data[index]:#돌면서 가장 최소값인 거와 바꾼다.(swap한다)
#기준점을 기준으로 돌고 끝까지 돌면서 가장 최솟값을 뽑고 그 인덱스를 바꾼다.
lowest = index
data[lowest], data[stand] = data[stand], data[lowest]
return data
알고리즘 분석
- 반복문이 두 개 O($n^2$)
- 실제로 상세하게 계산하면, $\frac { n * (n - 1)}{ 2 }$
삽입 정렬 (insertion sort)
1. 삽입 정렬 (insertion sort) 란?
- 삽입 정렬은 두 번째 인덱스부터 시작
- 해당 인덱스(key 값) 앞에 있는 데이터(B)부터 비교해서 key 값이 더 작으면, B값을 뒤 인덱스로 복사
- 이를 key 값이 더 큰 데이터를 만날때까지 반복, 그리고 큰 데이터를 만난 위치 바로 뒤에 key 값을 이동
직접 눈으로 보면 더 이해가 쉽다: https://visualgo.net/en/sorting
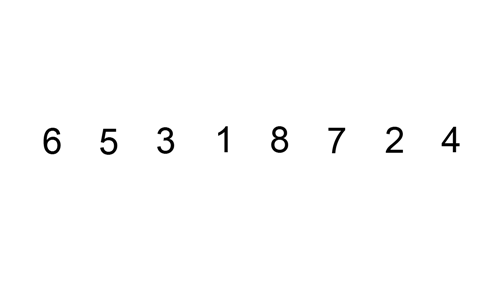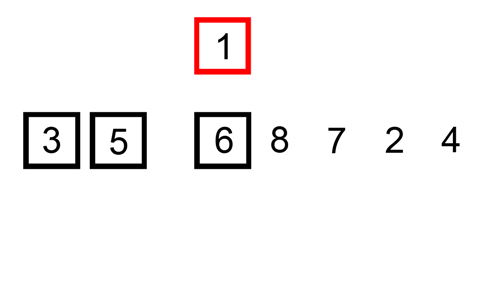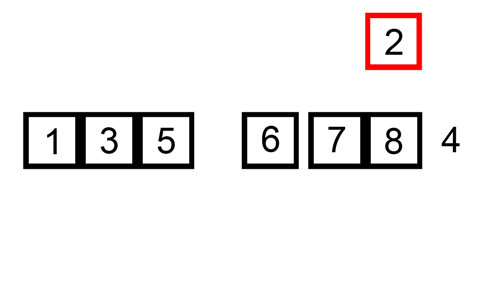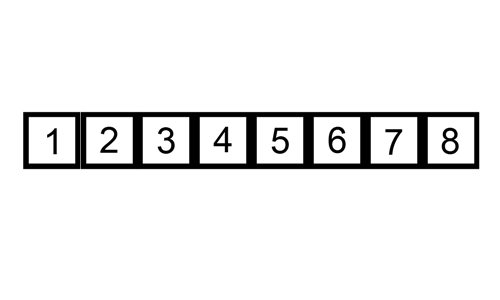
출처: https://commons.wikimedia.org/wiki/File:Insertion-sort-example.gif
- 데이터가 네 개 일때 (데이터 갯수에 따라 복잡도가 떨어지는 것은 아니므로, 네 개로 바로 로직을 이해해보자.)
- 예: data_list = [9, 3, 2, 5]
- 처음 한번 실행하면, key값은 9, 인덱스(0) - 1 은 0보다 작으므로 끝: [9, 3, 2, 5]
- 두 번째 실행하면, key값은 3, 9보다 3이 작으므로 자리 바꾸고, 끝: [3, 9, 2, 5]
- 세 번째 실행하면, key값은 2, 9보다 2가 작으므로 자리 바꾸고, 다시 3보다 2가 작으므로 끝: [2, 3, 9, 5]
- 네 번째 실행하면, key값은 5, 9보다 5이 작으므로 자리 바꾸고, 3보다는 5가 크므로 끝: [2, 3, 5, 9]
- 예: data_list = [9, 3, 2, 5]
알고리즘 구현
- for stand in range(len(data_list)) 로 반복
- key = data_list[stand]
- for num in range(stand, 0, -1) 반복
- 내부 반복문 안에서 data_list[stand] < data_list[num - 1] 이면,
- data_list[num - 1], data_list[num] = data_list[num], data_list[num - 1]
- 내부 반복문 안에서 data_list[stand] < data_list[num - 1] 이면,
def insertion_sort(data):
for index in range(len(data) - 1):#각 턴에서 어떻게 처리되냐
for index2 in range(index + 1, 0, -1):#여기서 0대신 -1을 쓰면 완전히 다른값 나올 수 있게 되므로 0쓴다.
#인덱스 번호+1에서 0까지 -1로 돌면서(배열 맨뒤에서 맨 앞으로 옮겨가면서 대신 맨앞은 고정(채워지므로 +1로 기준점 바뀌어감)
if data[index2] < data[index2 - 1]: #swap
#데이터의 인덱스 번호와 -1(0으로 가서 판단)
data[index2], data[index2 - 1] = data[index2 - 1], data[index2]
else:#만약 데이터가 2 3 5 4 에서 2345 로 되고 3 4 비교한뒤 3<4이면 4랑 2를 비교할 필요 없이 멈춘다. 그떄 break로 탈출
break
return data
4. 알고리즘 분석
- 반복문이 두 개 O($n^2$)
- 최악의 경우, $\frac { n * (n - 1)}{ 2 }$
완전 정렬이 되어 있는 상태라면 최선은 O(n)
- 이해가 안가면, 이 코드를 보면서 이해하기: https://goo.gl/XKBXuk
재귀 용법 (recursive call, 재귀 호출)
고급 정렬 알고리즘엥서 재귀 용법을 사용하므로, 고급 정렬 알고리즘을 익히기 전에 재귀 용법을 먼저 익히기로 합니다.
재귀 용법 (recursive call, 재귀 호출)
- 함수 안에서 동일한 함수를 호출하는 형태
- 여러 알고리즘 작성시 사용되므로, 익숙해져야 함
재귀 용법 이해
- 예제를 풀어보며, 재귀 용법을 이해해보기
예제 - 팩토리얼
- 간단한 경우부터 생각해보기
- 2! = 1 X 2
- 3! = 1 X 2 X 3
- 4! = 1 X 2 X 3 X 4 = 4 X 3!
- 규칙이 보임: n! = n X (n - 1)!
- 함수를 하나 만든다.
- 함수(n) 은 n > 1 이면 return n X 함수(n - 1)
- 함수(n) 은 n = 1 이면 return n
- 검증 (코드로 검증하지 않고, 직접 간단한 경우부터 대입해서 검증해야 함)
- 먼저 2! 부터
- 함수(2) 이면, 2 > 1 이므로 2 X 함수(1)
- 함수(1) 은 1 이므로, return 2 X 1 = 2 맞다!
- 함수(2) 이면, 2 > 1 이므로 2 X 함수(1)
- 먼저 3! 부터
- 함수(3) 이면, 3 > 1 이므로 3 X 함수(2)
- 함수(2) 는 결국 1번에 의해 2! 이므로, return 2 X 1 = 2
- 3 X 함수(2) = 3 X 2 = 3 X 2 X 1 = 6 맞다!
- 함수(3) 이면, 3 > 1 이므로 3 X 함수(2)
- 먼저 4! 부터
- 함수(4) 이면, 4 > 1 이므로 4 X 함수(3)
- 함수(3) 은 결국 2번에 의해 3 X 2 X 1 = 6
- 4 X 함수(3) = 4 X 6 = 24 맞다!
- 함수(4) 이면, 4 > 1 이므로 4 X 함수(3)
- 먼저 2! 부터
def factorial(num):
if num > 1:
return num * factorial(num - 1)
else:
return num
예제 - 시간 복잡도와 공간 복잡도
factorial(n) 은 n - 1 번의 factorial() 함수를 호출해서, 곱셈을 함
- 일종의 n-1번 반복문을 호출한 것과 동일
- factorial() 함수를 호출할 때마다, 지역변수 n 이 생성됨
시간 복잡도/공간 복잡도는 O(n-1) 이므로 결국, 둘 다 O(n)
일반적인 형태1
def function(입력):
if 입력 > 일정값: # 입력이 일정 값 이상이면
return function(입력 - 1) # 입력보다 작은 값
else:
return 일정값, 입력값, 또는 특정값 # 재귀 호출 종료
일반적인 형태2
def function(입력):
if 입력 <= 일정값: # 입력이 일정 값보다 작으면
return 일정값, 입력값, 또는 특정값 # 재귀 호출 종료
function(입력보다 작은 값)
return 결과값
팩토리얼 코드
def factorial(num):
if num <= 1:
return num
return num * factorial(num - 1)
재귀 호출은 스택의 전형적인 예
- 함수는 내부적오르 스택처럼 관리된다.
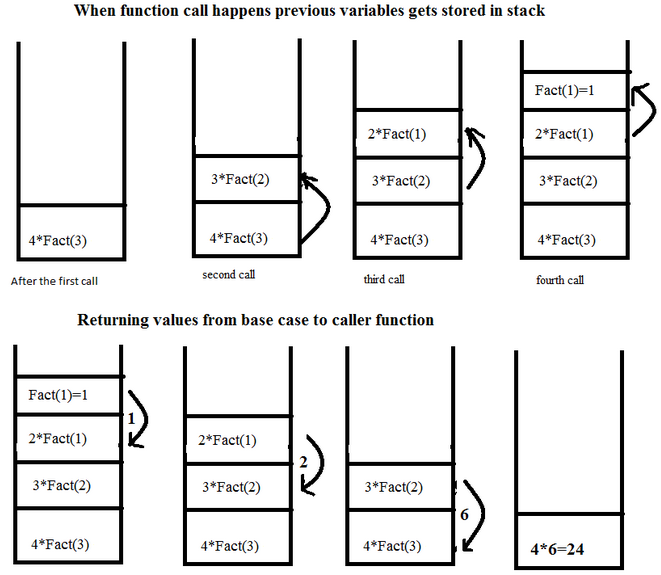
- 재귀 호출이 이해가 가지 않는다면? - 코드분석
참고: 파이썬에서 재귀 함수는 깊이가(한번에 호출되는…) 1000회 이하가 되어야 함
재귀 용법 연습문제
다음 함수를 재귀 함수를 활용해서 완성해서 1부터 num까지의 곱이 출력되게 만드세요
def muliple(data):
if data <= 1:
return data
return -------------------------
multiple(10)
</pre>
</div>
A1.
def multiple(num):
return_value = 1
for index in range(1, num + 1):
return_value = return_value * index
return return_value
A2.
def multiple(num):
if num <= 1:
return num
return num * multiple(num - 1)
숫자가 들어 있는 리스트가 주어졌을 때, 리스트의 합을 리턴하는 함수를 만드세요 (재귀함수를 써보세요)
def sum_list(data):
if len(data) == 1:
return data[0]
return --------------------------------
import random
data = random.sample(range(100), 10)
print (sum_list(data))
</pre>
A.
def sum_list(data):
if len(data) <= 1:
return data[0]
return data[0] + sum_list(data[1:])
회문(palindrome)은 순서를 거꾸로 읽어도 제대로 읽은 것과 같은 단어와 문장을 의미함 회문을 판별할 수 있는 함수를 재귀함수를 활용해서 만들어봅니다.
A.
def palindrome(string):
if len(strung) <= 1:
return True
if string[0] == string[-1]:
return palindrome(string[1:-1])
else:
return False
# 참고 - 리스트 슬라이싱
# string = 'Dave'
# string[-1] --> e
# string[0] --> D
# string[1:-1] --> av
# string[:-1] --> Dav
- 정수 n에 대해
- n이 홀수이면 3 X n + 1 을 하고,
- n이 짝수이면 n 을 2로 나눕니다.
- 이렇게 계속 진행해서 n 이 결국 1이 될 때까지 2와 3의 과정을 반복합니다.
예를 들어 n에 3을 넣으면,
3 10 5 16 8 4 2 1
이렇게 정수 n을 입력받아, 위 알고리즘에 의해 1이 되는 과정을 모두 출력하는 함수를 작성하세요.
A.
def func(n):
print (n)
if n == 1:
return n
if n % 2 == 1:
return (func((3 * n) + 1))
else:
return (func(int(n / 2)))
문제: 정수 4를 1, 2, 3의 조합으로 나타내는 방법은 다음과 같이 총 7가지가 있음 1+1+1+1 1+1+2 1+2+1 2+1+1 2+2 1+3 3+1 정수 n이 입력으로 주어졌을 때, n을 1, 2, 3의 합으로 나타낼 수 있는 방법의 수를 구하시오
힌트: 정수 n을 만들 수 있는 경우의 수를 리턴하는 함수를 f(n) 이라고 하면,
f(n)은 f(n-1) + f(n-2) + f(n-3) 과 동일하다는 패턴 찾기
문제 분석을 연습장에 작성해 본 예
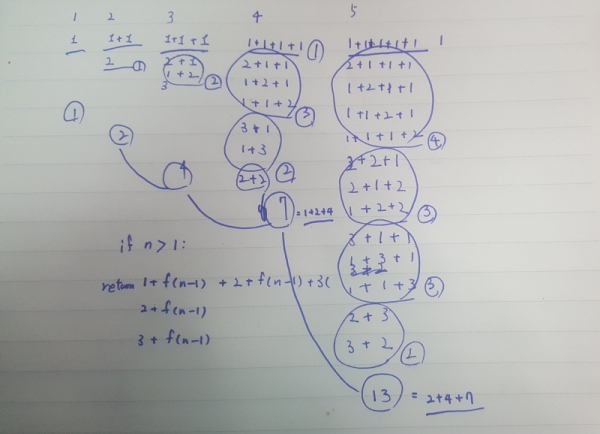
A.
def func(data):
if data == 1:
return 1
elif data == 2:
return 2
elif data == 3:
return 4
return func(data -1) + func(data - 2) + func(data - 3)
.
동적 계획법 (Dynamic Programming)과 분할 정복 (Divide and Conquer)
원래 문제를 작은 문제로 나누어서 해결
정의
- 동적계획법 (DP 라고 많이 부름)
- 입력 크기가 작은 부분 문제들을 해결한 후, 해당 부분 문제의 해를 활용해서, 보다 큰 크기의 부분 문제를 해결, 최종적으로 전체 문제를 해결하는 알고리즘
- 상향식 접근법으로, 가장 최하위 해답을 구한 후, 이를 저장하고, 해당 결과값을 이용해서 상위 문제를 풀어가는 방식
- Memoization 기법을 사용함
- Memoization (메모이제이션) 이란: 프로그램 실행 시 이전에 계산한 값을 저장하여, 다시 계산하지 않도록 하여 전체 실행 속도를 빠르게 하는 기술
- 문제를 잘게 쪼갤 때, 부분 문제는 중복되어, 재활용됨
- 예: 피보나치 수열
- 분할 정복
- 문제를 나눌 수 없을 때까지 나누어서 각각을 풀면서 다시 합병하여 문제의 답을 얻는 알고리즘
- 하양식 접근법으로, 상위의 해답을 구하기 위해, 아래로 내려가면서 하위의 해답을 구하는 방식
- 일반적으로 재귀함수로 구현
- 문제를 잘게 쪼갤 때, 부분 문제는 서로 중복되지 않음
- 예: 병합 정렬, 퀵 정렬 등
공통점과 차이점
- 공통점
- 문제를 잘게 쪼개서, 가장 작은 단위로 분할
- 차이점
- 동적 계획법
- 부분 문제는 중복되어, 상위 문제 해결 시 재활용됨
- Memoization 기법 사용 (부분 문제의 해답을 저장해서 재활용하는 최적화 기법으로 사용)
- 분할 정복
- 부분 문제는 서로 중복되지 않음
- Memoization 기법 사용 안함
- 동적 계획법
동적계획법 분할정복 둘다 문제를 작은 문제로 쪼갠다는 장점이 있다.
동적 계획법 알고리즘 이해
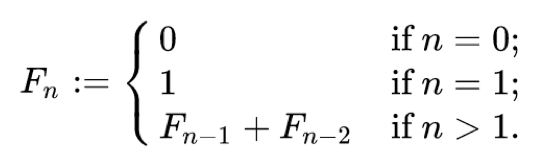
함수를 fibonacci 라고 하면, fibonacci(0):0 fibonacci(1):1 fibonacci(2):1 fibonacci(3):2 fibonacci(4):3 fibonacci(5):5 fibonacci(6):8 fibonacci(7):13 fibonacci(8):21 fibonacci(9):34
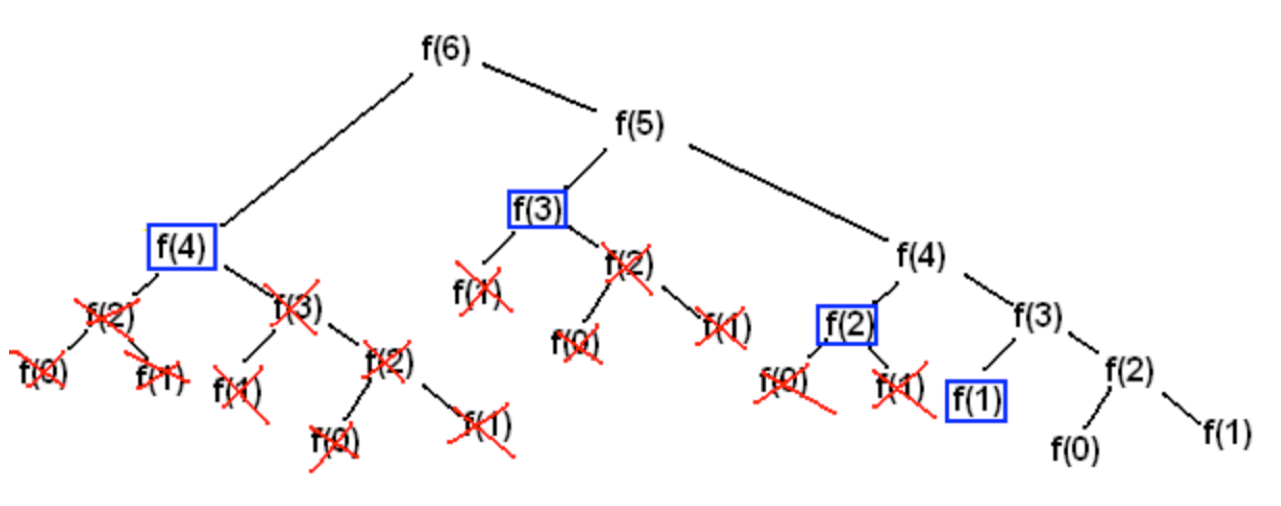
recursive call 활용
def fibo(num):
if num <= 1:
return num
return fibo(num - 1) + fibo(num - 2)
동적 계획법 활용
def fibo_dp(num):
cache = [ 0 for index in range(num + 1)]
cache[0] = 0
cache[1] = 1
for index in range(2, num + 1):
cache[index] = cache[index - 1] + cache[index - 2]
return cache[num]
실행 코드를 보며 이해해보기: 코드분석
분할 정복 알고리즘의 예는 병합 정렬과 퀵 정렬을 통해 이해
퀵 정렬 (quick sort)
퀵 정렬 (quick sort) 이란?
- 정렬 알고리즘의 꽃
- 기준점(pivot 이라고 부름)을 정해서, 기준점보다 작은 데이터는 왼쪽(left), 큰 데이터는 오른쪽(right) 으로 모으는 함수를 작성함
- 각 왼쪽(left), 오른쪽(right)은 재귀용법을 사용해서 다시 동일 함수를 호출하여 위 작업을 반복함
- 함수는 왼쪽(left) + 기준점(pivot) + 오른쪽(right) 을 리턴함
코드 구현
다음 리스트를 리스트 슬라이싱(예 [:2])을 이용해서 세 개로 짤라서 각 리스트 변수에 넣고 출력해보기
data_list = [1, 2, 3, 4, 5] 출력: print (data1) print (data2) print (data3) [1, 2] 3 [4, 5]
다음 리스트를 맨 앞에 데이터를 기준으로 작은 데이터는 left 변수에, 그렇지 않은 데이터는 right 변수에 넣기
data_list = [4, 1, 2, 5, 7]
다음 리스트를 맨 앞에 데이터를 pivot 변수에 넣고, pivot 변수 값을 기준으로 작은 데이터는 left 변수에, 그렇지 않은 데이터는 right 변수에 넣기
data_list 가 임의 길이일 때 리스트를 맨 앞에 데이터를 기준으로 작은 데이터는 left 변수에, 그렇지 않은 데이터는 right 변수에 넣기
import random
data_list = random.sample(range(100), 10)
left = list()
right = list()
pivot = data_list[0]
for index in range(1, -----------------):
if data_list[index] <pre pivot:
left.append(data_list[index])
else:
right.append(data_list[index])
data_list 가 다음 세 데이터를 가지고 있을 때 리스트를 맨 앞에 데이터를 기준으로 작은 데이터는 left 변수에, 그렇지 않은 데이터는 right 변수에 넣고 left, right, pivot 변수 값을 사용해서 정렬된 데이터 출력해보기
data_list = [4, 3, 2]

알고리즘 구현
- quicksort 함수 만들기
- 만약 리스트 갯수가 한개이면 해당 리스트 리턴
- 그렇지 않으면, 리스트 맨 앞의 데이터를 기준점(pivot)으로 놓기
- left, right 리스트 변수를 만들고,
- 맨 앞의 데이터를 뺀 나머지 데이터를 기준점과 비교(pivot)
- 기준점보다 작으면 left.append(해당 데이터)
- 기준점보다 크면 right.append(해당 데이터)
- return quicksort(left) + pivot + quicksort(right) 로 재귀 호출
리스트로 만들어서 리턴하기: return quick_sort(left) + [pivot] + quick_sort(right)
def qsort(data):
if len(data) <= 1:
return data
left, right = list(), list()
pivot = data[0]
for index in range(1, len(data)):
if pivot > data[index]:#피벗이 데이터의 인덱스보다 크다면(왼쪽에 있음)
left.append(data[index])
else:#아니면 오른쪽에 있음(피벗이 데이터 인덱스보다 크거나 같다면)
right.append(data[index])
return qsort(left) + [pivot] + qsort(right)
병합 정렬 (merge sort)
- 재귀용법을 활용한 정렬 알고리즘
- 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.
직접 눈으로 보면 더 이해가 쉽다: https://visualgo.net/en/sorting

출처: 위키피디아

알고리즘 이해
- 데이터가 네 개 일때 (데이터 갯수에 따라 복잡도가 떨어지는 것은 아니므로, 네 개로 바로 로직을 이해해보자.)
- 예: data_list = [1, 9, 3, 2]
- 먼저 [1, 9], [3, 2] 로 나누고
- 다시 앞 부분은 [1], [9] 로 나누고
- 다시 정렬해서 합친다. [1, 9]
- 다음 [3, 2] 는 [3], [2] 로 나누고
- 다시 정렬해서 합친다 [2, 3]
- 이제 [1, 9] 와 [2, 3]을 합친다.
- 1 < 2 이니 [1]
- 9 > 2 이니 [1, 2]
- 9 > 3 이니 [1, 2, 3]
- 9 밖에 없으니, [1, 2, 3, 9]
- 예: data_list = [1, 9, 3, 2]
알고리즘 구현
mergesplit 함수 만들기
- 만약 리스트 갯수가 한개이면 해당 값 리턴
- 그렇지 않으면, 리스트를 앞뒤, 두 개로 나누기
- left = mergesplit(앞)
- right = mergesplit(뒤)
- merge(left, right)
merge 함수 만들기
- 리스트 변수 하나 만들기 (sorted)
- left_index, right_index = 0
- while left_index < len(left) or right_index < len(right):
- 만약 left_index 나 right_index 가 이미 left 또는 right 리스트를 다 순회했다면, 그 반대쪽 데이터를 그대로 넣고, 해당 인덱스 1 증가
- if left[left_index] < right[right_index]:
- sorted.append(left[left_index])
- left_index += 1
- else:
- sorted.append(right[right_index])
- right_index += 1
.
def merge(left, right):
merged = list()
left_point, right_point = 0, 0
# case1 - left/right 둘다 있을때
while len(left) > left_point and len(right) > right_point:
if left[left_point] > right[right_point]:
merged.append(right[right_point])
right_point += 1
else:
merged.append(left[left_point])
left_point += 1
# case2 - left 데이터가 없을 때
while len(left) > left_point:
merged.append(left[left_point])
left_point += 1
# case3 - right 데이터가 없을 때
while len(right) > right_point:
merged.append(right[right_point])
right_point += 1
return merged
def mergesplit(data):
if len(data) <= 1:
return data
medium = int(len(data) / 2)
left = mergesplit(data[:medium])
right = mergesplit(data[medium:])
return merge(left, right)
알고리즘 분석
- 알고리즘 분석은 쉽지 않음, 이 부분은 참고로만 알아두자.
- 다음을 보고 이해해보자
- 몇 단계 깊이까지 만들어지는지를 depth 라고 하고 i로 놓자. 맨 위 단계는 0으로 놓자.
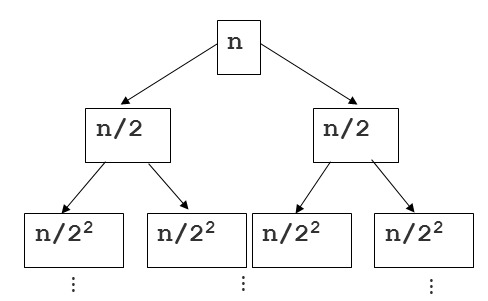
- 다음 그림에서 n/$2^2$ 는 2단계 깊이라고 해보자.
- 각 단계에 있는 하나의 노드 안의 리스트 길이는 n/$2^2$ 가 된다.
- 각 단계에는 $2^i$ 개의 노드가 있다.
- 따라서, 각 단계는 항상 $2^i * \frac { n }{ 2^i } = O(n)$
- 단계는 항상 $log_2 n$ 개 만큼 만들어짐, 시간 복잡도는 결국 O(log n), 2는 역시 상수이므로 삭제
- 따라서, 단계별 시간 복잡도 O(n) * O(log n) = O(n log n)
- 몇 단계 깊이까지 만들어지는지를 depth 라고 하고 i로 놓자. 맨 위 단계는 0으로 놓자.
- 다음을 보고 이해해보자
이진 탐색 (Binary Search)
이진 탐색 (Binary Search) 이란?
- 탐색할 자료를 둘로 나누어 해당 데이터가 있을만한 곳을 탐색하는 방법
예시 문제

이진 탐색의 이해 (순차 탐색과 비교하며 이해하기)
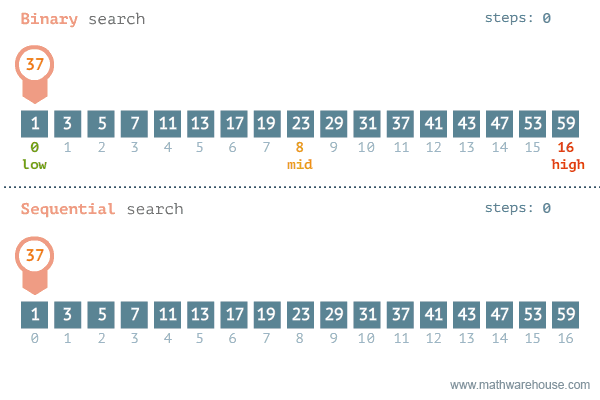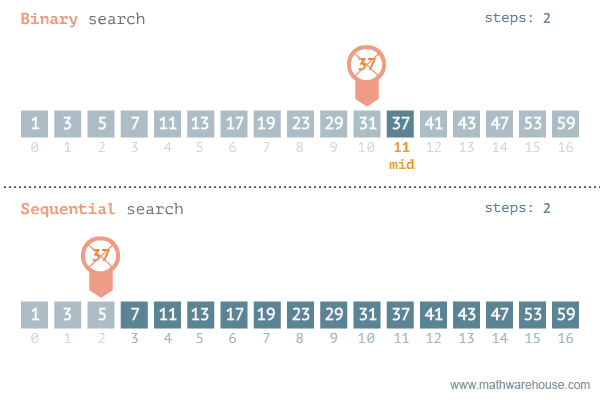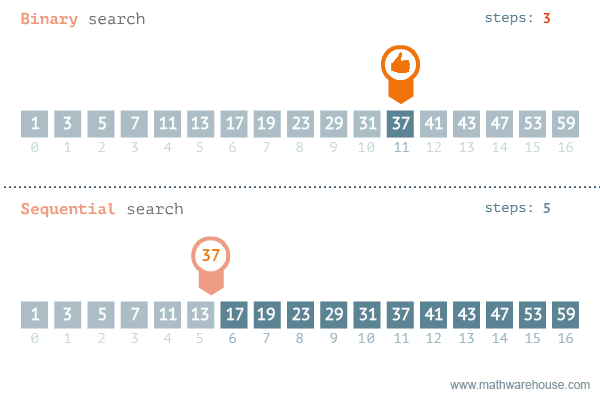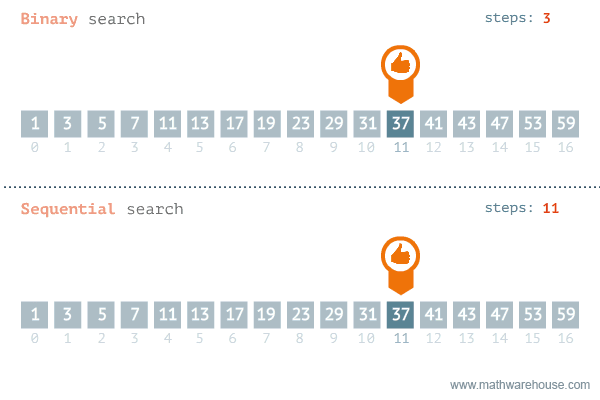
- [저작자] by penjee.com 이미지 출처
분할 정복 알고리즘과 이진 탐색
무한도전때 티켓 찾는거라 생각하면 된다 . 100-> 50->25-> 37->43 (솨십솨)
- 분할 정복 알고리즘 (Divide and Conquer)
- Divide: 문제를 하나 또는 둘 이상으로 나눈다.
- Conquer: 나눠진 문제가 충분히 작고, 해결이 가능하다면 해결하고, 그렇지 않다면 다시 나눈다.
- 이진 탐색
- Divide: 리스트를 두 개의 서브 리스트로 나눈다.
- Comquer
- 검색할 숫자 (search) > 중간값 이면, 뒷 부분의 서브 리스트에서 검색할 숫자를 찾는다.
- 검색할 숫자 (search) < 중간값 이면, 앞 부분의 서브 리스트에서 검색할 숫자를 찾는다.
어떻게 코드로 만들까?
- 이진 탐색은 데이터가 정렬되있는 상태에서 진행
- 데이터가 [2, 3, 8, 12, 20] 일 때,
- binary_search(data_list, find_data) 함수를 만들고
- find_data는 찾는 숫자
- data_list는 데이터 리스트
- data_list의 중간값을 find_data와 비교해서
- find_data < data_list의 중간값 이라면
- 맨 앞부터 data_list의 중간까지 에서 다시 find_data 찾기
- data_list의 중간값 < find_data 이라면
- data_list의 중간부터 맨 끝까지에서 다시 find_data 찾기
- 그렇지 않다면, data_list의 중간값은 find_data 인 경우로, return data_list 중간위치
- find_data < data_list의 중간값 이라면
- binary_search(data_list, find_data) 함수를 만들고
def binary_search(data, search):
print (data)
if len(data) == 1 and search == data[0]:
return True #1인 경우 데이터 리턶나는게 아니라 만약 서치하는게 마나 확인
#만약 데이터가 1개 밖에 없다면 그게 내가 검색한 거인지 보고 아니면 검색하려는게 존재하지 않는 것이다.
if len(data) == 1 and search != data[0]:
return False
if len(data) == 0:
return False
medium = len(data) // 2 #분할정복진행
if search == data[medium]:#만약 서치로 데이터 찾으면
return True
else:
if search > data[medium]: #서치가 데이터 찾는거보다 크면(오른쪽 탐색)
return binary_search(data[medium+1:], search)
else:#반대로 왼쪽 탐색 서치가 찾는 데이터보다 작으면
return binary_search(data[:medium], search)
알고리즘 분석
n개의 리스트를 매번 2로 나누어 1이 될 때까지 비교연산을 k회 진행
- n X $\frac { 1 }{ 2 }$ X $\frac { 1 }{ 2 }$ X $\frac { 1 }{ 2 }$ ... = 1
- n X $\frac { 1 }{ 2 }^k$ = 1
- n = $2^k$ = $log_2 n$ = $log_2 2^k$
- $log_2 n$ = k
- 빅 오 표기법으로는 k + 1 이 결국 최종 시간 복잡도임 (1이 되었을 때도, 비교연산을 한번 수행)
- 결국 O($log_2 n$ + 1) 이고, 2와 1, 상수는 삭제 되므로, O($log n$)
순차 탐색 (Sequential Search)
순차 탐색 (Sequential Search) 이란?
- 탐색은 여러 데이터 중에서 원하는 데이터를 찾아내는 것을 의미
데이터가 담겨있는 리스트를 앞에서부터 하나씩 비교해서 원하는 데이터를 찾는 방법
- 그냥 가장 기본적인 알고리즘이다.
from random import *
rand_data_list = list()
for num in range(10):
rand_data_list.append(randint(1, 100))
rand_data_list
def sequencial(data_list, search_data):
for index in range(len(data_list)):
if data_list[index] == search_data:
return index
return -1
sequencial(rand_data_list, 4)
알고리즘 분석
- 최악의 경우 리스트 길이가 n일 때, n번 비교해야 함
- O(n)
그래프 이해
그래프 (Graph) 란?
- 그래프는 실제 세계의 현상이나 사물을 정점(Vertex) 또는 노드(Node) 와 간선(Edge)로 표현하기 위해 사용
예제 집에서 회사로 가는 경로를 그래프로 표현한 예
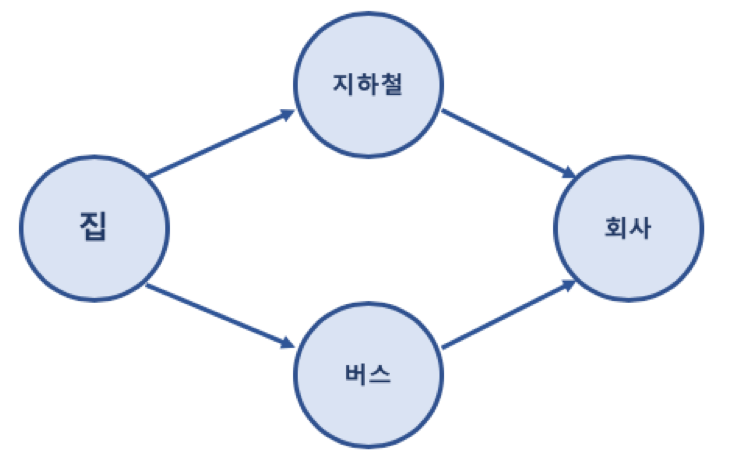
그래프 (Graph) 관련 용어
- 노드 (Node): 위치를 말함, 정점(Vertex)라고도 함
- 간선 (Edge): 위치 간의 관계를 표시한 선으로 노드를 연결한 선이라고 보면 됨 (link 또는 branch 라고도 함)
- 인접 정점 (Adjacent Vertex) : 간선으로 직접 연결된 정점(또는 노드)
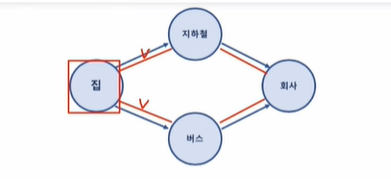
여기서 집의 간선은 2개이다. 여기서 지하철에 들어오는 간선(진입차선) 은 1개 지하철에서 나가는 간선도 1개. 경로길이는 집에서 회사 가는데 경로길이는 간선길이로 2개의 간선이 사용되었으며 경로길이는 2이다.
집에서 회사 가는건 단순 경로지만(중복된 정점이 없음) 집에서 집 오는건 사이클이 될 수 있다. 출발지와 목적지에 따라 단순경로, 사이클이 될 수 있다.
근데 집->집 처럼 처음과 끝이 중복은 허용한다(단순 경로로 본다.)
집->집 오는 건 단순경로로 볼수도 있고 싸이클로 볼 수도 있다.(단순경로도 맞고 출발지==목적지라 사이클로 불러도 맞는 말이다.)
- 참고 용어
- 정점의 차수 (Degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수
- 진입 차수 (In-Degree): 방향 그래프에서 외부에서 오는 간선의 수
- 진출 차수 (Out-Degree): 방향 그래프에서 외부로 향하는 간선의 수
- 경로 길이 (Path Length): 경로를 구성하기 위해 사용된 간선의 수
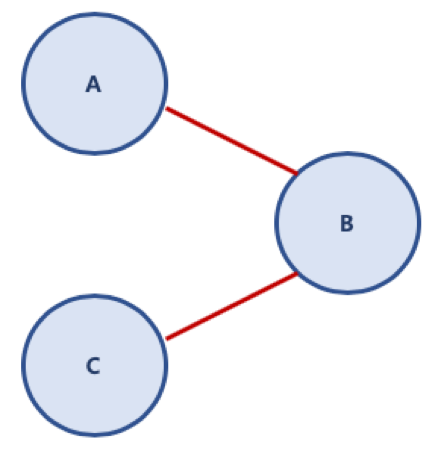
- 단순 경로 (Simple Path): 처음 정점과 끝 정점을 제외하고 중복된 정점이 없는 경로
- 사이클 (Cycle): 단순 경로의 시작 정점과 종료 정점이 동일한 경우
단순 경로 (A - B - C)
그래프 (Graph) 종류
무방향 그래프 (Undirected Graph)
- 방향이 없는 그래프
- 간선을 통해, 노드는 양방향으로 갈 수 있음
- 보통 노드 A, B가 연결되어 있을 경우, (A, B) 또는 (B, A) 로 표기
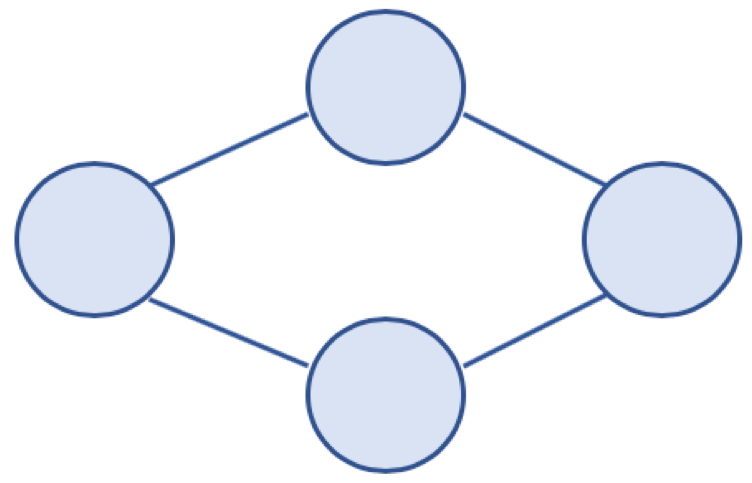
방향 그래프 (Directed Graph)
- 간선에 방향이 있는 그래프
- 보통 노드 A, B가 A -> B 로 가는 간선으로 연결되어 있을 경우, <A, B> 로 표기 (<B, A> 는 B -> A 로 가는 간선이 있는 경우이므로 <A, B> 와 다름)
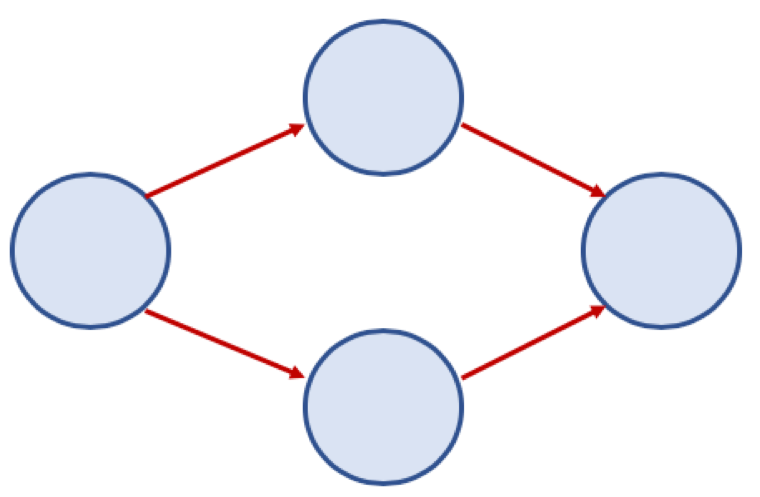
가중치 그래프 (Weighted Graph) 또는 네트워크 (Network)
- 간선에 비용 또는 가중치가 할당된 그래프
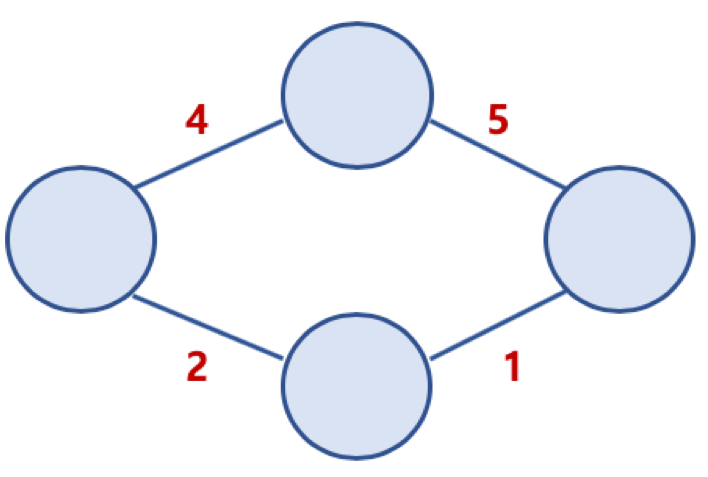
연결 그래프 (Connected Graph) 와 비연결 그래프 (Disconnected Graph)
- 연결 그래프 (Connected Graph)
- 무방향 그래프에 있는 모든 노드에 대해 항상 경로가 존재하는 경우
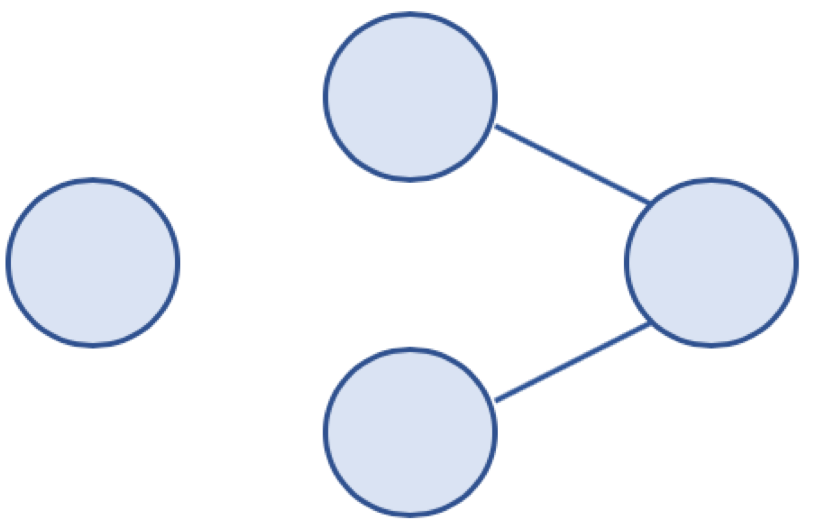
- 비연결 그래프 (Disconnected Graph)
- 무방향 그래프에서 특정 노드에 대해 경로가 존재하지 않는 경우
비연결 그래프 예
사이클 (Cycle) 과 비순환 그래프 (Acyclic Graph)
- 사이클 (Cycle)
- 단순 경로의 시작 노드와 종료 노드가 동일한 경우
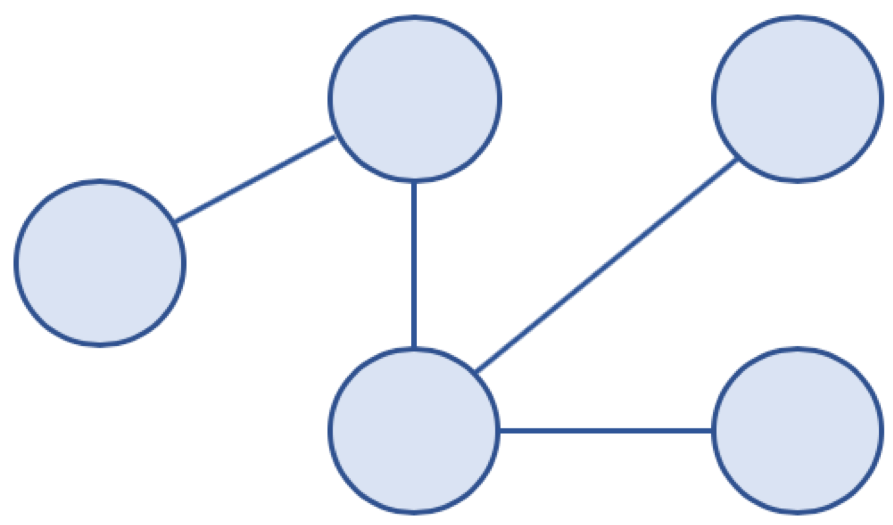
- 비순환 그래프 (Acyclic Graph)
- 사이클이 없는 그래프
비순환 그래프 예
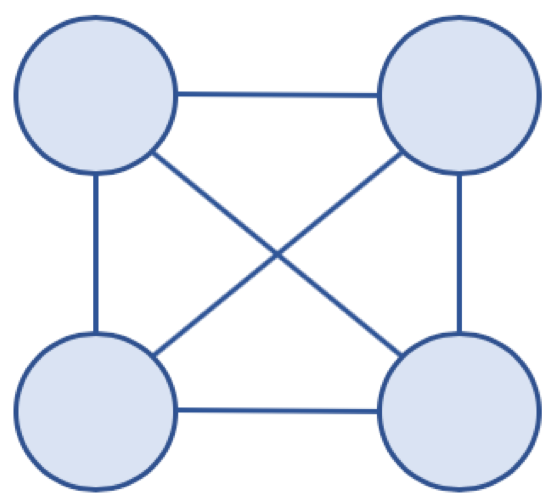
완전 그래프 (Complete Graph)
- 그래프의 모든 노드가 서로 연결되어 있는 그래프
완전 그래프 예
그래프와 트리의 차이
- 트리는 그래프 중에 속한 특별한 종류라고 볼 수 있음
| 그래프 | 트리 | |
|---|---|---|
| 정의 | 노드와 노드를 연결하는 간선으로 표현되는 자료 구조 | 그래프의 한 종류, 방향성이 있는 비순환 그래프 |
| 방향성 | 방향 그래프, 무방향 그래프 둘다 존재함 | 방향 그래프만 존재함 |
| 사이클 | 사이클 가능함, 순환 및 비순환 그래프 모두 존재함 | 비순환 그래프로 사이클이 존재하지 않음 |
| 루트 노드 | 루트 노드 존재하지 않음 | 루트 노드 존재함 |
| 부모/자식 관계 | 부모 자식 개념이 존재하지 않음 | 부모 자식 관계가 존재함 |
깊이 우선 탐색 (Depth-First Search)
BFS 와 DFS 란?
- 대표적인 그래프 탐색 알고리즘
- 너비 우선 탐색 (Breadth First Search): 정점들과 같은 레벨에 있는 노드들 (형제 노드들)을 먼저 탐색하는 방식
- 깊이 우선 탐색 (Depth First Search): 정점의 자식들을 먼저 탐색하는 방식
BFS/DFS 방식 이해를 위한 예제
- BFS 방식: A - B - C - D - G - H - I - E - F - J
- 한 단계씩 내려가면서, 해당 노드와 같은 레벨에 있는 노드들 (형제 노드들)을 먼저 순회함
- DFS 방식: A - B - D - E - F - C - G - H - I - J
- 한 노드의 자식을 타고 끝까지 순회한 후, 다시 돌아와서 다른 형제들의 자식을 타고 내려가며 순화함
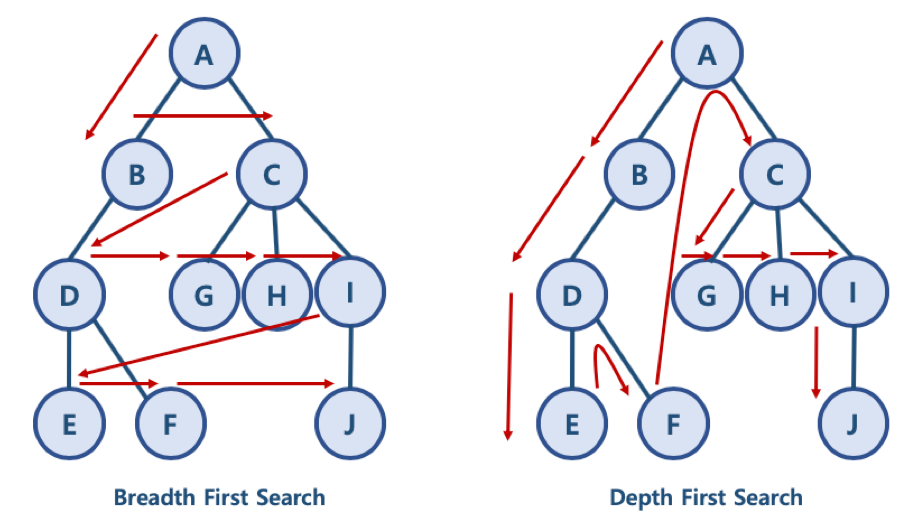
파이썬으로 그래프를 표현하는 방법
- 파이썬에서 제공하는 딕셔너리와 리스트 자료 구조를 활용해서 그래프를 표현할 수 있음
graph = dict()
graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']
그래프 예와 파이썬 표현
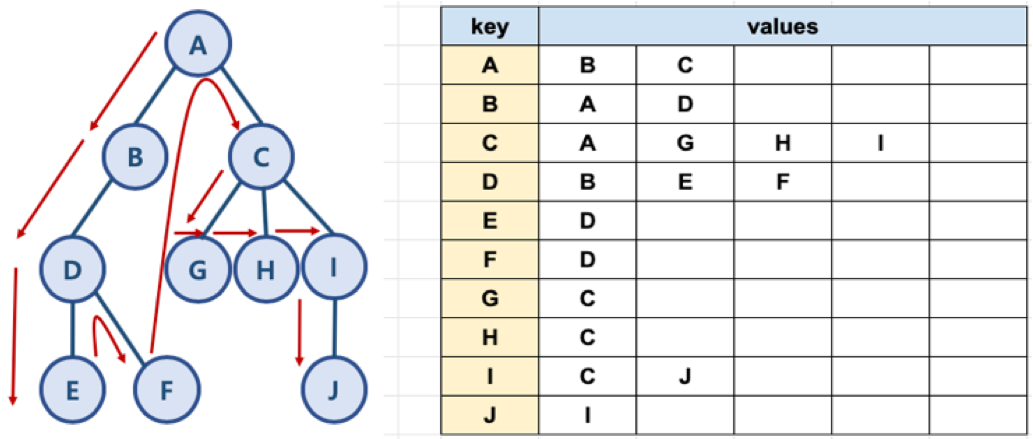
DFS 알고리즘 구현
- 자료구조 스택과 큐를 활용함
- need_visit 스택과 visited 큐, 두 개의 자료 구조를 생성
BFS 자료구조는 두 개의 큐를 활용하는데 반해, DFS 는 스택과 큐를 활용한다는 차이가 있음을 인지해야 함
- 큐와 스택 구현은 별도 라이브러리를 활용할 수도 있지만, 간단히 파이썬 리스트를 활용할 수도 있음
def dfs(graph, start_node):
visited, need_visit = list(), list()
need_visit.append(start_node)
while need_visit:
node = need_visit.pop()
if node not in visited:
visited.append(node)
need_visit.extend(graph[node])
return visited
4. 시간 복잡도
- 일반적인 DFS 시간 복잡도
- 노드 수: V
- 간선 수: E
- 위 코드에서 while need_visit 은 V + E 번 만큼 수행함
- 시간 복잡도: O(V + E)
너비 우선 탐색 (Breadth-First Search)
BFS 와 DFS 란?
- 대표적인 그래프 탐색 알고리즘
- 너비 우선 탐색 (Breadth First Search): 정점들과 같은 레벨에 있는 노드들 (형제 노드들)을 먼저 탐색하는 방식
- 깊이 우선 탐색 (Depth First Search): 정점의 자식들을 먼저 탐색하는 방식
BFS/DFS 방식 이해를 위한 예제
- BFS 방식: A - B - C - D - G - H - I - E - F - J
- 한 단계씩 내려가면서, 해당 노드와 같은 레벨에 있는 노드들 (형제 노드들)을 먼저 순회함
- DFS 방식: A - B - D - E - F - C - G - H - I - J
- 한 노드의 자식을 타고 끝까지 순회한 후, 다시 돌아와서 다른 형제들의 자식을 타고 내려가며 순화함

파이썬으로 그래프를 표현하는 방법
- 파이썬에서 제공하는 딕셔너리와 리스트 자료 구조를 활용해서 그래프를 표현할 수 있음
그래프 예와 파이썬 표현
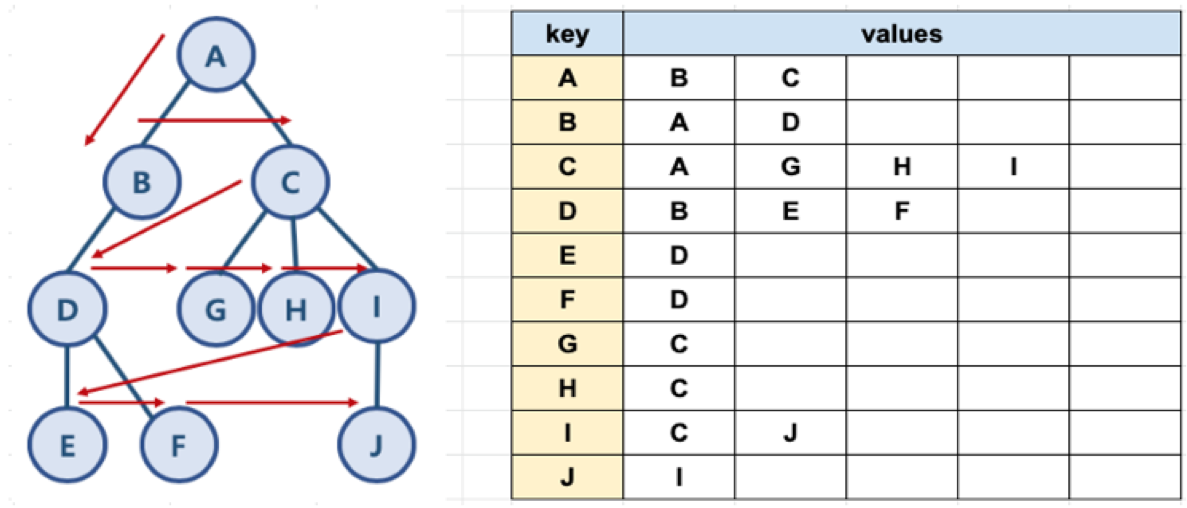
graph = dict()
graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']
BFS 알고리즘 구현
- 자료구조 큐를 활용함
- need_visit 큐와 visited 큐, 두 개의 큐를 생성
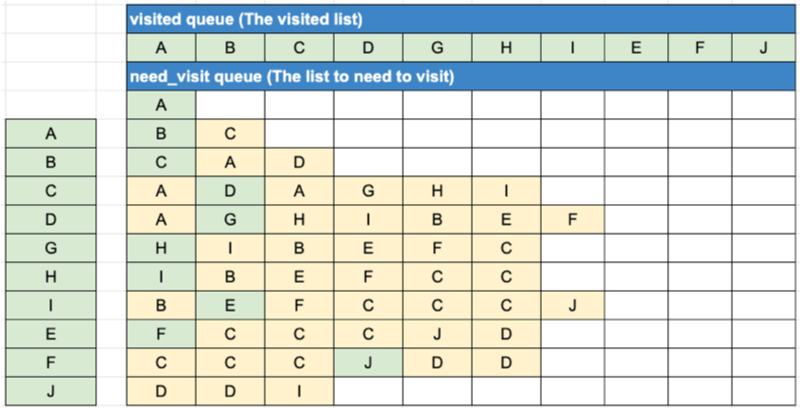
- 큐의 구현은 간단히 파이썬 리스트를 활용
def bfs(graph, start_node):
visited = list()
need_visit = list()
need_visit.append(start_node)
while need_visit:
node = need_visit.pop(0)
if node not in visited:
visited.append(node)
need_visit.extend(graph[node])
return visited

4. 시간 복잡도
- 일반적인 BFS 시간 복잡도
- 노드 수: V
- 간선 수: E
- 위 코드에서 while need_visit 은 V + E 번 만큼 수행함
- 시간 복잡도: O(V + E)
def bfs(graph, start_node):
visited = list()
need_visit = list()
need_visit.append(start_node)
count = 0
while need_visit:
count += 1
node = need_visit.pop(0)
if node not in visited:
visited.append(node)
need_visit.extend(graph[node])
print (count)
return visited
백 트래킹 기법의 이해
백 트래킹 (backtracking)
- 백트래킹 (backtracking) 또는 퇴각 검색 (backtrack)으로 부름
- 제약 조건 만족 문제 (Constraint Satisfaction Problem) 에서 해를 찾기 위한 전략
- 해를 찾기 위해, 후보군에 제약 조건을 점진적으로 체크하다가, 해당 후보군이 제약 조건을 만족할 수 없다고 판단되는 즉시 backtrack (다시는 이 후보군을 체크하지 않을 것을 표기)하고, 바로 다른 후보군으로 넘어가며, 결국 최적의 해를 찾는 방법
- 실제 구현시, 고려할 수 있는 모든 경우의 수 (후보군)를 상태공간트리(State Space Tree)를 통해 표현
- 각 후보군을 DFS 방식으로 확인
- 상태 공간 트리를 탐색하면서, 제약이 맞지 않으면 해의 후보가 될만한 곳으로 바로 넘어가서 탐색
- Promising: 해당 루트가 조건에 맞는지를 검사하는 기법
- Pruning (가지치기): 조건에 맞지 않으면 포기하고 다른 루트로 바로 돌아서서, 탐색의 시간을 절약하는 기법
즉, 백트래킹은 트리 구조를 기반으로 DFS로 깊이 탐색을 진행하면서 각 루트에 대해 조건에 부합하는지 체크(Promising), 만약 해당 트리(나무)에서 조건에 맞지않는 노드는 더 이상 DFS로 깊이 탐색을 진행하지 않고, 가지를 쳐버림 (Pruning)
상태 공간 트리 (State Space Tree)
- 문제 해결 과정의 중간 상태를 각각의 노드로 나타낸 트리
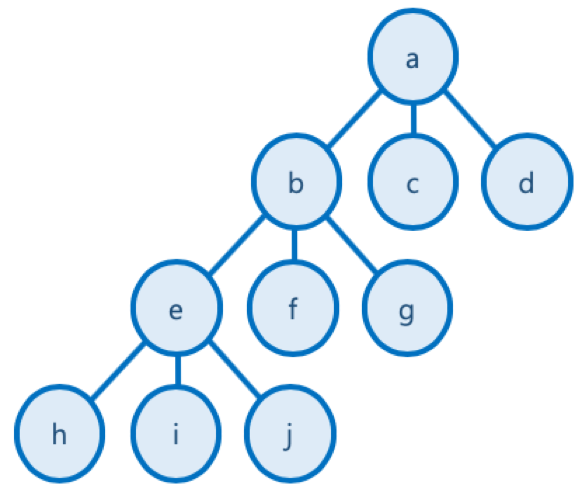
트리 형태를 만들어서 접근하는 거지 코드에서 트리를 직접 만들거나 하진 않는다.
N Queen 문제 이해
- 대표적인 백트래킹 문제
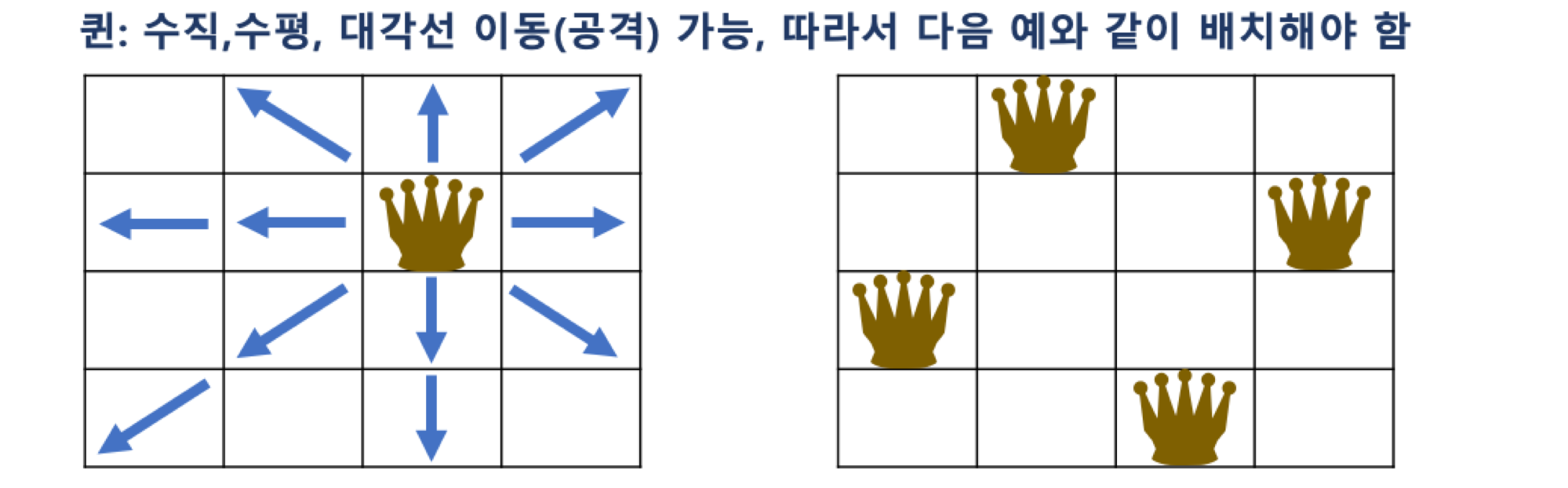
- NxN 크기의 체스판에 N개의 퀸을 서로 공격할 수 없도록 배치하는 문제
- 퀸은 다음과 같이 이동할 수 있으므로, 배치된 퀸 간에 공격할 수 없는 위치로 배치해야 함
Pruning (가지치기) for N Queen 문제
- 한 행에는 하나의 퀸 밖에 위치할 수 없음 (퀸은 수평 이동이 가능하므로)
- 맨 위에 있는 행부터 퀸을 배치하고, 다음 행에 해당 퀸이 이동할 수 없는 위치를 찾아 퀸을 배치
- 만약 앞선 행에 배치한 퀸으로 인해, 다음 행에 해당 퀸들이 이동할 수 없는 위치가 없을 경우에는, 더 이상 퀸을 배치하지 않고, 이전 행의 퀸의 배치를 바꿈
- 즉, 맨 위의 행부터 전체 행까지 퀸의 배치가 가능한 경우의 수를 상태 공간 트리 형태로 만든 후, 각 경우를 맨 위의 행부터 DFS 방식으로 접근, 해당 경우가 진행이 어려울 경우, 더 이상 진행하지 않고, 다른 경우를 체크하는 방식
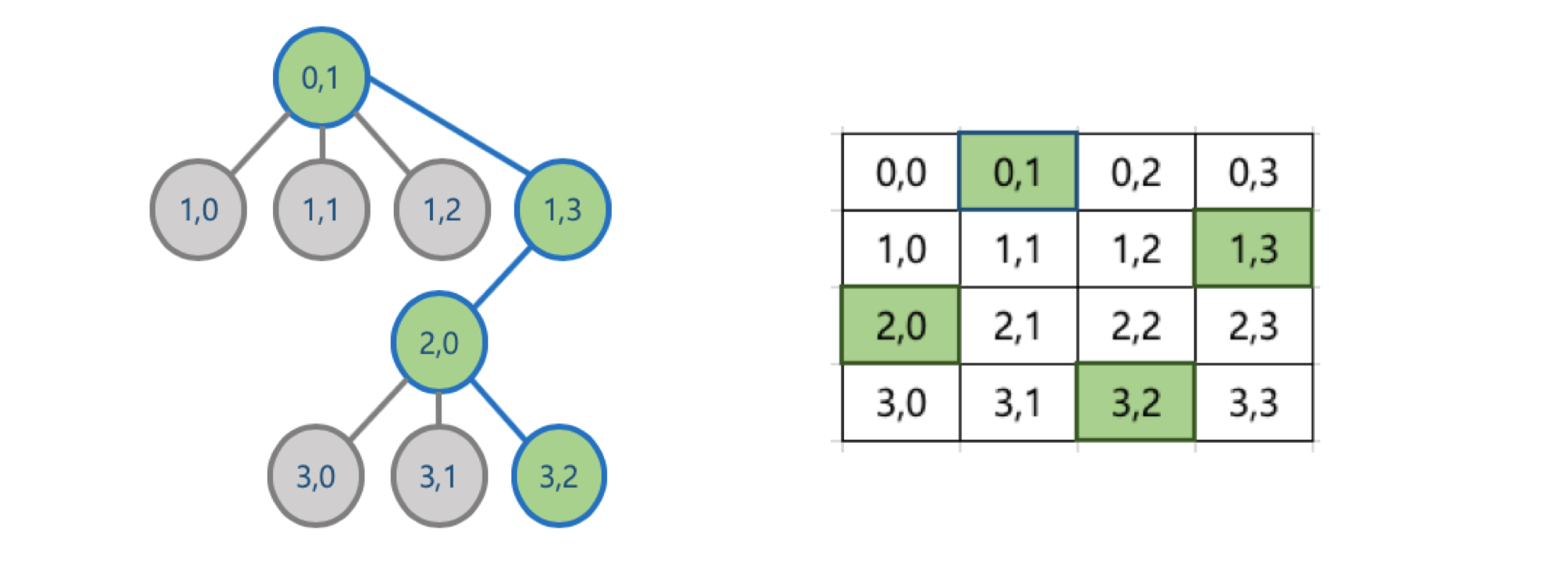
- 즉, 맨 위의 행부터 전체 행까지 퀸의 배치가 가능한 경우의 수를 상태 공간 트리 형태로 만든 후, 각 경우를 맨 위의 행부터 DFS 방식으로 접근, 해당 경우가 진행이 어려울 경우, 더 이상 진행하지 않고, 다른 경우를 체크하는 방식
Promising for N Queen 문제
- 해당 루트가 조건에 맞는지를 검사하는 기법을 활용하여,
- 현재까지 앞선 행에서 배치한 퀸이 이동할 수 없는 위치가 있는지를 다음과 같은 조건으로 확인
- 한 행에 어차피 하나의 퀸만 배치 가능하므로 수평 체크는 별도로 필요하지 않음
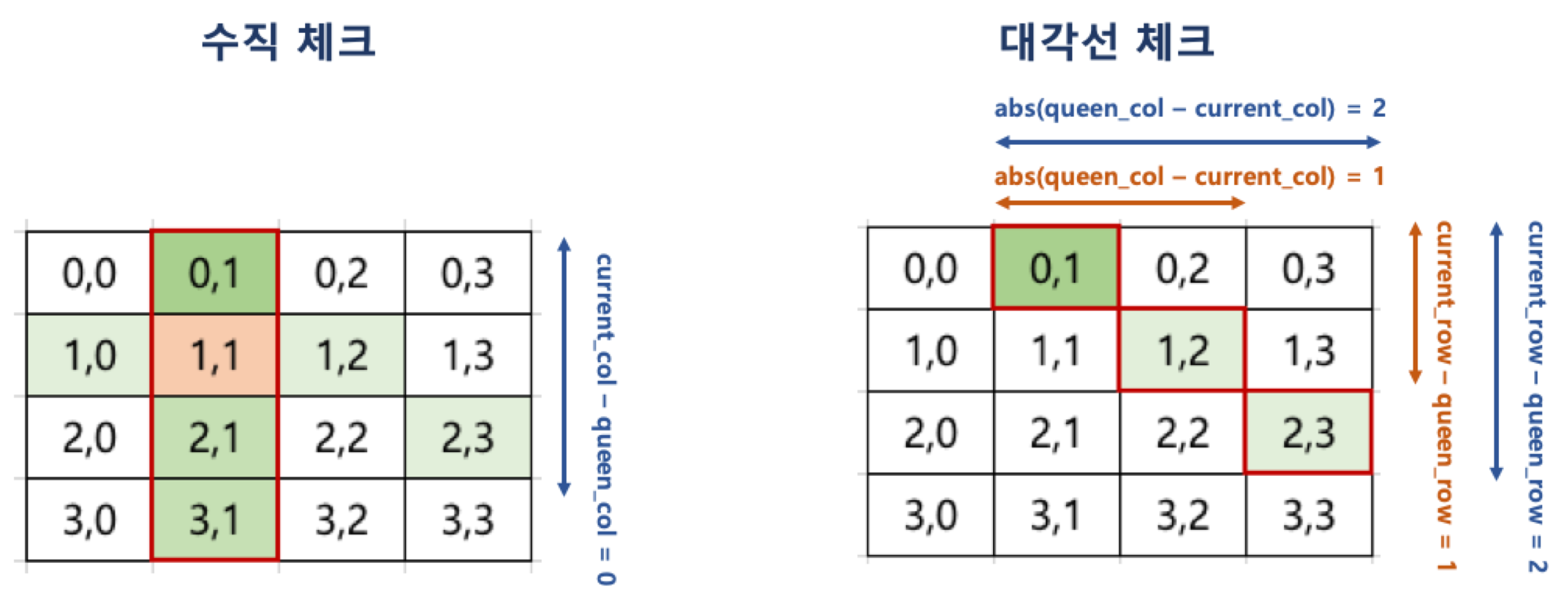
- 한 행에 어차피 하나의 퀸만 배치 가능하므로 수평 체크는 별도로 필요하지 않음
N Queen 문제 파이썬 코드 작성
def is_available(candidate, current_col):
current_row = len(candidate)#candidate 길이와 동일
for queen_row in range(current_row): #행이 0부터 시작
if candidate[queen_row] == current_col or abs(candidate[queen_row] - current_col) == current_row - queen_row:
#만약 여기서 둘중 하나라도 만족하게 되면
#queen row = 퀸의 컬럼 번호 current_col과 같은지(인자로 넘어온) 또는
#candidate의 queen의 row(z컬럼과)-current_row것의 조건이 맞다면 다음에 위치할 수 있는 경우는 안된다.
return False
return True#위 그림의 조건을 만족하지 않으면 그 자리에 퀸을 놓을 수 있으므로 true를 리턴하게 된다.
def DFS(N, current_row, current_candidate, final_result):
if current_row == N:
final_result.append(current_candidate[:])#얇은 복사(복사본 넘겨줌)
return
for candidate_col in range(N):#N개의 열이있고 0번부터 체크
if is_available(current_candidate, candidate_col):#리스트가 맨앞부터 들어감.
current_candidate.append(candidate_col)
DFS(N, current_row + 1, current_candidate, final_result)#그 다음행에 지금까지 배치된 걸 넘겨준다.
#만약 이걸하면 다시 넘어올텐데 마지막 행까지 가지도 않았고 다음 행에 4가지의 열이 하나도 조건 만족하지 않으면 아무 조건없이 리턴
#리턴 된다는 건 (아무거도 없이) 지금까지의 배치 조합으로는 그 다음행에 퀸 놓을 자리가 없다(백트랙)
current_candidate.pop()#가장 최근에 append된게 없어진다.
def solve_n_queens(N):
final_result = []
DFS(N, 0, [], final_result)
return final_result
탐욕 알고리즘(Greedey Algorithm)
탐욕 알고리즘 이란?
- Greedy algorithm 또는 탐욕 알고리즘 이라고 불리움
- 최적의 해에 가까운 값을 구하기 위해 사용됨
- 여러 경우 중 하나를 결정해야할 때마다, 매순간 최적이라고 생각되는 경우를 선택하는 방식으로 진행해서, 최종적인 값을 구하는 방식
탐욕 알고리즘 예
문제1: 동전 문제
- 지불해야 하는 값이 4720원 일 때 1원 50원 100원, 500원 동전으로 동전의 수가 가장 적게 지불하시오.
- 가장 큰 동전부터 최대한 지불해야 하는 값을 채우는 방식으로 구현 가능
- 탐욕 알고리즘으로 매순간 최적이라고 생각되는 경우를 선택하면 됨
coin_list = [500, 100, 50, 1]
def min_coin_count(value, coin_list):
total_coin_count = 0
details = list()
coin_list.sort(reverse=True)
for coin in coin_list:
coin_num = value // coin
total_coin_count += coin_num
value -= coin_num * coin
details.append([coin, coin_num])
return total_coin_count, details
#####: 부분 배낭 문제 (Fractional Knapsack Problem)
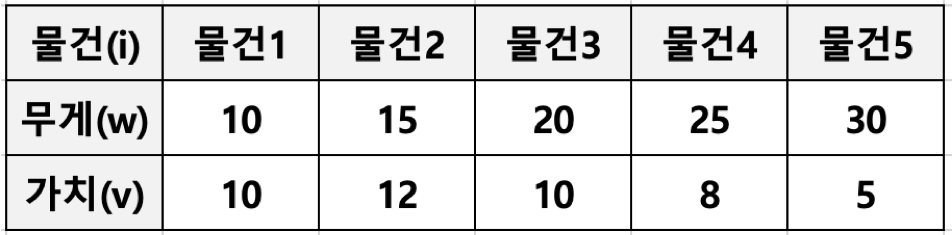
- 무게 제한이 k인 배낭에 최대 가치를 가지도록 물건을 넣는 문제
- 각 물건은 무게(w)와 가치(v)로 표현될 수 있음
- 물건은 쪼갤 수 있으므로 물건의 일부분이 배낭에 넣어질 수 있음, 그래서 Fractional Knapsack Problem 으로 부름
- Fractional Knapsack Problem 의 반대로 물건을 쪼개서 넣을 수 없는 배낭 문제도 존재함 (0/1 Knapsack Problem 으로 부름)
- Fractional Knapsack Problem 의 반대로 물건을 쪼개서 넣을 수 없는 배낭 문제도 존재함 (0/1 Knapsack Problem 으로 부름)
def get_max_value(data_list, capacity):
data_list = sorted(data_list, key=lambda x: x[1] / x[0], reverse=True)
total_value = 0
details = list()
for data in data_list:
if capacity - data[0] >= 0:
capacity -= data[0]
total_value += data[1]
details.append([data[0], data[1], 1])
else:
fraction = capacity / data[0]
total_value += data[1] * fraction
details.append([data[0], data[1], fraction])
break
return total_value, details
탐욕 알고리즘의 한계
- 탐욕 알고리즘은 근사치 추정에 활용
- 반드시 최적의 해를 구할 수 있는 것은 아니기 때문
- 최적의 해에 가까운 값을 구하는 방법 중의 하나임
예
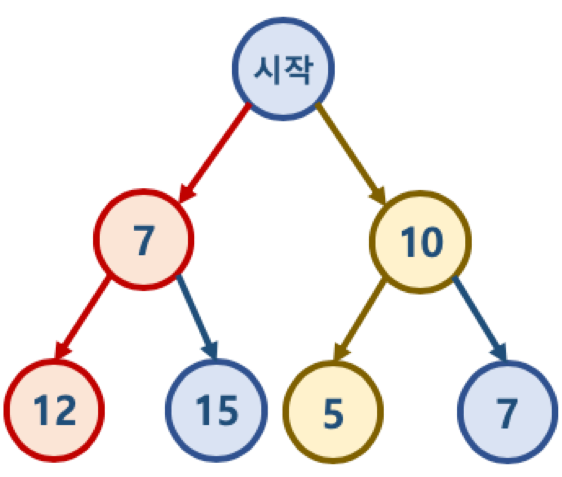
- ‘시작’ 노드에서 시작해서 가장 작은 값을 찾아 leaf node 까지 가는 경로를 찾을 시에
- Greedy 알고리즘 적용시 시작 -> 7 -> 12 를 선택하게 되므로 7 + 12 = 19 가 됨
- 하지만 실제 가장 작은 값은 시작 -> 10 -> 5 이며, 10 + 5 = 15 가 답
최단 경로 문제란?
- 최단 경로 문제란 두 노드를 잇는 가장 짧은 경로를 찾는 문제임
- 가중치 그래프 (Weighted Graph) 에서 간선 (Edge)의 가중치 합이 최소가 되도록 하는 경로를 찾는 것이 목적
최단 경로 문제 종류
- 단일 출발 및 단일 도착 (single-source and single-destination shortest path problem) 최단 경로 문제
- 그래프 내의 특정 노드 u 에서 출발, 또다른 특정 노드 v 에 도착하는 가장 짧은 경로를 찾는 문제
- 단일 출발 (single-source shortest path problem) 최단 경로 문제
- 그래프 내의 특정 노드 u 와 그래프 내 다른 모든 노드 각각의 가장 짧은 경로를 찾는 문제
따지고 보면 굉장히 헷깔릴 수 있으므로 명확히 하자면, 예를 들어 A, B, C, D 라는 노드를 가진 그래프에서 특정 노드를 A 라고 한다면, A 외 모든 노드인 B, C, D 각 노드와 A 간에 (즉, A - B, A - C, A - D) 각각 가장 짧은 경로를 찾는 문제를 의미함
- 그래프 내의 특정 노드 u 와 그래프 내 다른 모든 노드 각각의 가장 짧은 경로를 찾는 문제
- 전체 쌍(all-pair) 최단 경로: 그래프 내의 모든 노드 쌍 (u, v) 에 대한 최단 경로를 찾는 문제
최단 경로 알고리즘 - 다익스트라 알고리즘
- 다익스트라 알고리즘은 위의 최단 경로 문제 종류 중, 2번에 해당
- 하나의 정점에서 다른 모든 정점 간의 각각 가장 짧은 거리를 구하는 문제
다익스트라 알고리즘 로직
- 첫 정점을 기준으로 연결되어 있는 정점들을 추가해 가며, 최단 거리를 갱신하는 기법
- 다익스트라 알고리즘은 너비우선탐색(BFS)와 유사
- 첫 정점부터 각 노드간의 거리를 저장하는 배열을 만든 후, 첫 정점의 인접 노드 간의 거리부터 먼저 계산하면서, 첫 정점부터 해당 노드간의 가장 짧은 거리를 해당 배열에 업데이트
다익스트라 알고리즘의 다양한 변형 로직이 있지만, 가장 개선된 우선순위 큐를 사용하는 방식에 집중해서 설명하기로 함
- 첫 정점부터 각 노드간의 거리를 저장하는 배열을 만든 후, 첫 정점의 인접 노드 간의 거리부터 먼저 계산하면서, 첫 정점부터 해당 노드간의 가장 짧은 거리를 해당 배열에 업데이트
- 우선순위 큐를 활용한 다익스트라 알고리즘
- 우선순위 큐는 MinHeap 방식을 활용해서, 현재 가장 짧은 거리를 가진 노드 정보를 먼저 꺼내게 됨
1) 첫 정점을 기준으로 배열을 선언하여 첫 정점에서 각 정점까지의 거리를 저장
- 초기에는 첫 정점의 거리는 0, 나머지는 무한대로 저장함 (inf 라고 표현함)
- 우선순위 큐에 (첫 정점, 거리 0) 만 먼저 넣음
2) 우선순위 큐에서 노드를 꺼냄
- 처음에는 첫 정점만 저장되어 있으므로, 첫 정점이 꺼내짐
- 첫 정점에 인접한 노드들 각각에 대해, 첫 정점에서 각 노드로 가는 거리와 현재 배열에 저장되어 있는 첫 정점에서 각 정점까지의 거리를 비교한다.
- 배열에 저장되어 있는 거리보다, 첫 정점에서 해당 노드로 가는 거리가 더 짧을 경우, 배열에 해당 노드의 거리를 업데이트한다.
- 배열에 해당 노드의 거리가 업데이트된 경우, 우선순위 큐에 넣는다.
- 결과적으로 너비 우선 탐색 방식과 유사하게, 첫 정점에 인접한 노드들을 순차적으로 방문하게 됨
- 만약 배열에 기록된 현재까지 발견된 가장 짧은 거리보다, 더 긴 거리(루트)를 가진 (노드, 거리)의 경우에는 해당 노드와 인접한 노드간의 거리 계산을 하지 않음
3) 2번의 과정을 우선순위 큐에 꺼낼 노드가 없을 때까지 반복한다.
예제로 이해하는 다익스트라 알고리즘 (우선순위 큐 활용)
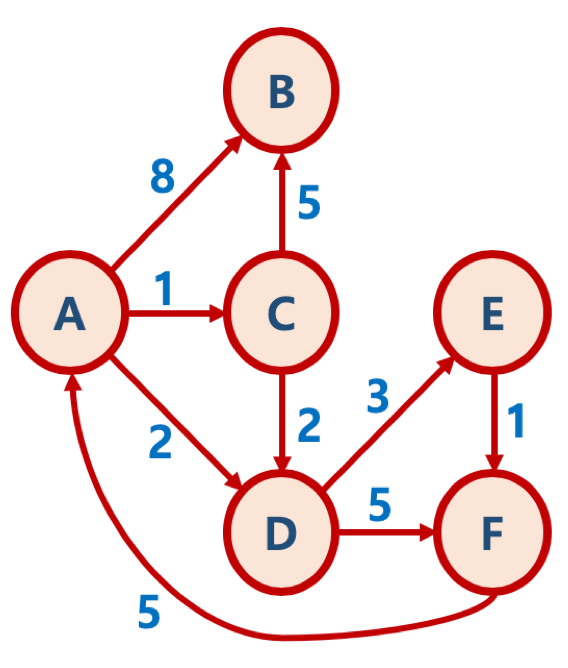
정점을 기준으로 우선순위 큐를 이용해서 너비우선탐색(BFS를 실시한다.) 최단거리정보가 배열에 업데이트 되면그 업데이트 된 노드와 거리정보는 우선순위 큐에 들어가서 반복하면서 가장 거리가 작은 순부터 출발점과 해당거리 계산한다.
이 과정은 우선순위 큐에 업데이트 없을 떄 까지 반복한다.
1단계: 초기화
- 첫 정점을 기준으로 배열을 선언하여 첫 정점에서 각 정점까지의 거리를 저장
- 파이썬으로 하면 리스트가 될 수 있다.
- 초기에는 첫 정점의 거리는 0, 나머지는 무한대로 저장함 (inf 라고 표현함)
- 우선순위 큐에 (첫 정점, 거리 0) 만 먼저 넣음

2단계: 우선순위 큐에서 추출한 (A, 0) [노드, 첫 노드와의 거리] 를 기반으로 인접한 노드와의 거리 계산
- 우선순위 큐에서 노드를 꺼냄
- 처음에는 첫 정점만 저장되어 있으므로, 첫 정점이 꺼내짐
- 첫 정점에 인접한 노드들 각각에 대해, 첫 정점에서 각 노드로 가는 거리와 현재 배열에 저장되어 있는 첫 정점에서 각 정점까지의 거리를 비교한다.
- 배열에 저장되어 있는 거리보다, 첫 정점에서 해당 노드로 가는 거리가 더 짧을 경우, 배열에 해당 노드의 거리를 업데이트한다.
- 배열에 해당 노드의 거리가 업데이트된 경우, 우선순위 큐에 넣는다.
- 결과적으로 너비 우선 탐색 방식과 유사하게, 첫 정점에 인접한 노드들을 순차적으로 방문하게 됨
- 만약 배열에 기록된 현재까지 발견된 가장 짧은 거리보다, 더 긴 거리(루트)를 가진 (노드, 거리)의 경우에는 해당 노드와 인접한 노드간의 거리 계산을 하지 않음
이전 표에서 보듯이, 첫 정점 이외에 모두 inf 였었으므로, 첫 정점에 인접한 노드들은 모두 우선순위 큐에 들어가고, 첫 정점과 인접한 노드간의 거리가 배열에 업데이트됨
큐에서 하나 노드 꺼내서 인접 노드간 거리 계산하고 그 값이 배열에 저장된 값보다 작으면 배열 업데이트 해주고 우선순위 쿨
우선순위 들어가는 시간 순서에 관계없이,1보단 2가 커서 우선순위 들어가는 관계 없이 1부터 pop(됨(시간순서 낮은거))
2단계 부터는 반복문 계속 돈다고 보면 좋다. 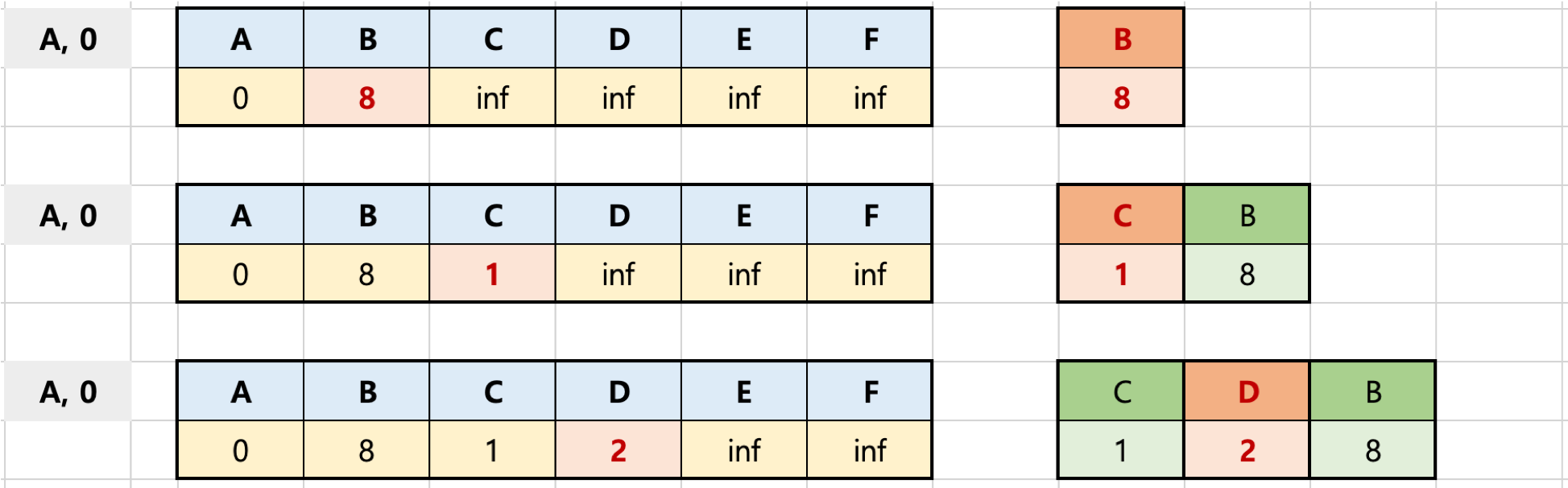
3단계: 우선순위 큐에서 (C, 1) [노드, 첫 노드와의 거리] 를 기반으로 인접한 노드와의 거리 계산
- 우선순위 큐가 MinHeap(최소 힙) 방식이므로, 위 표에서 넣어진 (C, 1), (D, 2), (B, 8) 중 (C, 1) 이 먼저 추출됨 (pop)
- 위 표에서 보듯이 1단계까지의 A - B 최단 거리는 8 인 상황임
- A - C 까지의 거리는 1, C 에 인접한 B, D에서 C - B는 5, 즉 A - C - B 는 1 + 5 = 6 이므로, A - B 최단 거리 8보다 더 작은 거리를 발견, 이를 배열에 업데이트
- 배열에 업데이트했으므로 B, 6 (즉 A에서 B까지의 현재까지 발견한 최단 거리) 값이 우선순위 큐에 넣어짐
- C - D 의 거리는 2, 즉 A - C - D 는 1 + 2 = 3 이므로, A - D의 현재 최단 거리인 2 보다 긴 거리, 그래서 D 의 거리는 업데이트되지 않음
c1이라는 노드 정보 가지고 다 C의 노드가 접근할 수 있는 인접노드간의 거리 계산.
- A - C 까지의 거리는 1, C 에 인접한 B, D에서 C - B는 5, 즉 A - C - B 는 1 + 5 = 6 이므로, A - B 최단 거리 8보다 더 작은 거리를 발견, 이를 배열에 업데이트
C에서 갈수있는건 B (거리계산)

4단계: 우선순위 큐에서 (D, 2) [노드, 첫 노드와의 거리] 를 기반으로 인접한 노드와의 거리 계산
- 지금까지 접근하지 못했던 E와 F 거리가 계산됨
- A - D 까지의 거리인 2 에 D - E 가 3 이므로 이를 더해서 E, 5
- A - D 까지의 거리인 2 에 D - F 가 5 이므로 이를 더해서 F, 7

5단계: 우선순위 큐에서 (E, 5) [노드, 첫 노드와의 거리] 를 기반으로 인접한 노드와의 거리 계산
- A - E 거리가 5인 상태에서, E에 인접한 F를 가는 거리는 1, 즉 A - E - F 는 5 + 1 = 6, 현재 배열에 A - F 최단거리가 7로 기록되어 있으므로, F, 6 으로 업데이트
- 우선순위 큐에 F, 6 추가

6단계: 우선순위 큐에서 (B, 6), (F, 6) 를 순차적으로 추출해 각 노드 기반으로 인접한 노드와의 거리 계산
- 예제의 방향 그래프에서 B 노드는 다른 노드로 가는 루트가 없음
- F 노드는 A 노드로 가는 루트가 있으나, 현재 A - A 가 0 인 반면에 A - F - A 는 6 + 5 = 11, 즉 더 긴 거리이므로 업데이트되지 않음

6단계: 우선순위 큐에서 (F, 7), (B, 8) 를 순차적으로 추출해 각 노드 기반으로 인접한 노드와의 거리 계산
- A - F 로 가는 하나의 루트의 거리가 7 인 상황이나, 배열에서 이미 A - F 로 가는 현재의 최단 거리가 6인 루트의 값이 있는 상황이므로, 더 긴거리인 F, 7 루트 기반 인접 노드까지의 거리는 계산할 필요가 없음, 그래서 계산없이 스킵함
- 계산하더라도 A - F 거리가 6인 루트보다 무조건 더 긴거리가 나올 수 밖에 없음
- B, 8 도 현재 A - B 거리가 6이므로, 인접 노드 거리 계산이 필요 없음.
우선순위 큐를 사용하면 불필요한 계산 과정을 줄일 수 있음
다익스트라 알고리즘 = 어떤 출발점 기준으로 그래프 노드간의 최단거리 구하는 알고리즘
어떻게 구하나? 전체 출발점과 각각 노드간의 최단거리 저장해둔 배열 만들고 출발점부터 시작해서 우선순위 큐 시작해서 출발점 부터 해당노드간의 최단거리, 루트 기억하는 최단거리 값과 노드를 저장하고 하나씩 뽑아서 해당노드와 연결된 최단거리 구해서 배열에 저된 최단거리보다 작으면 업데이트 하고 우선순위 큐에 넣고 크면 스킵
이걸 우선순위 큐에 끄집어 낼 데이터가 없을 때 까지 반복하면 결과적으로 맨 마지막에 출발점 노드간의 최단거리를 구할 수있다.

우선순위 큐 사용 장점
- 지금까지 발견된 가장 짧은 거리의 노드에 대해서 먼저 계산
- 더 긴 거리로 계산된 루트에 대해서는 계산을 스킵할 수 있음
heapq를 쓰면 파이썬에서 쉽게 만들 수 있다.
다익스트라 알고리즘 파이썬 구현 (우선순위 큐 활용까지 포함)
heapq 라이브러리 활용을 통해 우선순위 큐 사용하기
- 데이터가 리스트 형태일 경우, 0번 인덱스를 우선순위로 인지, 우선순위가 낮은 순서대로 pop 할 수 있음
import heapq
queue = []
heapq.heappush(queue, [2, 'A'])
heapq.heappush(queue, [5, 'B'])
heapq.heappush(queue, [1, 'C'])
heapq.heappush(queue, [7, 'D'])
print (queue)
for index in range(len(queue)):
print (heapq.heappop(queue))
다익스트라 알고리즘
- 탐색할 그래프의 시작 정점과 다른 정점들간의 최단 거리 구하기
mygraph = { ‘A’: {‘B’: 8, ‘C’: 1, ‘D’: 2}, ‘B’: {}, ‘C’: {‘B’: 5, ‘D’: 2}, ‘D’: {‘E’: 3, ‘F’: 5}, ‘E’: {‘F’: 1}, ‘F’: {‘A’: 5} }
import heapq
def dijkstra(graph, start):
distances = {node: float('inf') for node in graph}
distances[start] = 0
queue = []
heapq.heappush(queue, [distances[start], start])
while queue:
current_distance, current_node = heapq.heappop(queue)
if distances[current_node] < current_distance:
continue
for adjacent, weight in graph[current_node].items():
distance = current_distance + weight
if distance < distances[adjacent]:
distances[adjacent] = distance
heapq.heappush(queue, [distance, adjacent])
return distances

dijkstra(mygraph, ‘A’)
{‘A’: 0, ‘B’: 6, ‘C’: 1, ‘D’: 2, ‘E’: 5, ‘F’: 6}
참고: 최단 경로 출력
- 탐색할 그래프의 시작 정점과 다른 정점들간의 최단 거리 및 최단 경로 출력하기
import heapq
# 탐색할 그래프와 시작 정점을 인수로 전달받습니다.
def dijkstra(graph, start, end):
# 시작 정점에서 각 정점까지의 거리를 저장할 딕셔너리를 생성하고, 무한대(inf)로 초기화합니다.
distances = {vertex: [float('inf'), start] for vertex in graph}
# 그래프의 시작 정점의 거리는 0으로 초기화 해줌
distances[start] = [0, start]
# 모든 정점이 저장될 큐를 생성합니다.
queue = []
# 그래프의 시작 정점과 시작 정점의 거리(0)을 최소힙에 넣어줌
heapq.heappush(queue, [distances[start][0], start])
while queue:
# 큐에서 정점을 하나씩 꺼내 인접한 정점들의 가중치를 모두 확인하여 업데이트합니다.
current_distance, current_vertex = heapq.heappop(queue)
# 더 짧은 경로가 있다면 무시한다.
if distances[current_vertex][0] < current_distance:
continue
for adjacent, weight in graph[current_vertex].items():
distance = current_distance + weight
# 만약 시작 정점에서 인접 정점으로 바로 가는 것보다 현재 정점을 통해 가는 것이 더 가까울 경우에는
if distance < distances[adjacent][0]:
# 거리를 업데이트합니다.
distances[adjacent] = [distance, current_vertex]
heapq.heappush(queue, [distance, adjacent])
path = end
path_output = end + '->'
while distances[path][1] != start:
path_output += distances[path][1] + '->'
path = distances[path][1]
path_output += start
print (path_output)
return distances
# 방향 그래프
mygraph = {
'A': {'B': 8, 'C': 1, 'D': 2},
'B': {},
'C': {'B': 5, 'D': 2},
'D': {'E': 3, 'F': 5},
'E': {'F': 1},
'F': {'A': 5}
}
print(dijkstra(mygraph, 'A', 'F'))
시간 복잡도
- 위 다익스트라 알고리즘은 크게 다음 두 가지 과정을 거침
- 과정1: 각 노드마다 인접한 간선들을 모두 검사하는 과정
- 과정2: 우선순위 큐에 노드/거리 정보를 넣고 삭제(pop)하는 과정
- 각 과정별 시간 복잡도
- 과정1: 각 노드는 최대 한 번씩 방문하므로 (첫 노드와 해당 노드간의 갈 수 있는 루트가 있는 경우만 해당), 그래프의 모든 간선은 최대 한 번씩 검사
- 즉, 각 노드마다 인접한 간선들을 모두 검사하는 과정은 O(E) 시간이 걸림, E 는 간선(edge)의 약자
- 과정2: 우선순위 큐에 가장 많은 노드, 거리 정보가 들어가는 경우, 우선순위 큐에 노드/거리 정보를 넣고, 삭제하는 과정이 최악의 시간이 걸림
- 우선순위 큐에 가장 많은 노드, 거리 정보가 들어가는 시나리오는 그래프의 모든 간선이 검사될 때마다, 배열의 최단 거리가 갱신되고, 우선순위 큐에 노드/거리가 추가되는 것임
- 이 때 추가는 각 간선마다 최대 한 번 일어날 수 있으므로, 최대 O(E)의 시간이 걸리고, O(E) 개의 노드/거리 정보에 대해 우선순위 큐를 유지하는 작업은 $ O(log{E}) $ 가 걸림
- 따라서 해당 과정의 시간 복잡도는 $ O(Elog{E}) $
- 과정1: 각 노드는 최대 한 번씩 방문하므로 (첫 노드와 해당 노드간의 갈 수 있는 루트가 있는 경우만 해당), 그래프의 모든 간선은 최대 한 번씩 검사
총 시간 복잡도
- 과정1 + 과정2 = O(E) + $ O(Elog{E}) $ = $ O(E + Elog{E}) = O(Elog{E}) $
참고: 힙의 시간 복잡도
- depth (트리의 높이) 를 h라고 표기한다면,
- n개의 노드를 가지는 heap 에 데이터 삽입 또는 삭제시, 최악의 경우 root 노드에서 leaf 노드까지 비교해야 하므로 h=log2n 에 가까우므로, 시간 복잡도는 O(logn)
최소 신장 트리의 이해
신장 트리 란?
- Spanning Tree, 또는 신장 트리 라고 불리움 (Spanning Tree가 보다 자연스러워 보임)
- 원래의 그래프의 모든 노드가 연결되어 있으면서 트리의 속성을 만족하는 그래프
신장 트리의 조건
- 본래의 그래프의 모든 노드를 포함해야 함
- 모든 노드가 서로 연결
- 트리의 속성을 만족시킴 (사이클이 존재하지 않음)
모든 노드 연결하되 사이클이 존재하면 스패닝 트리가 아니다!
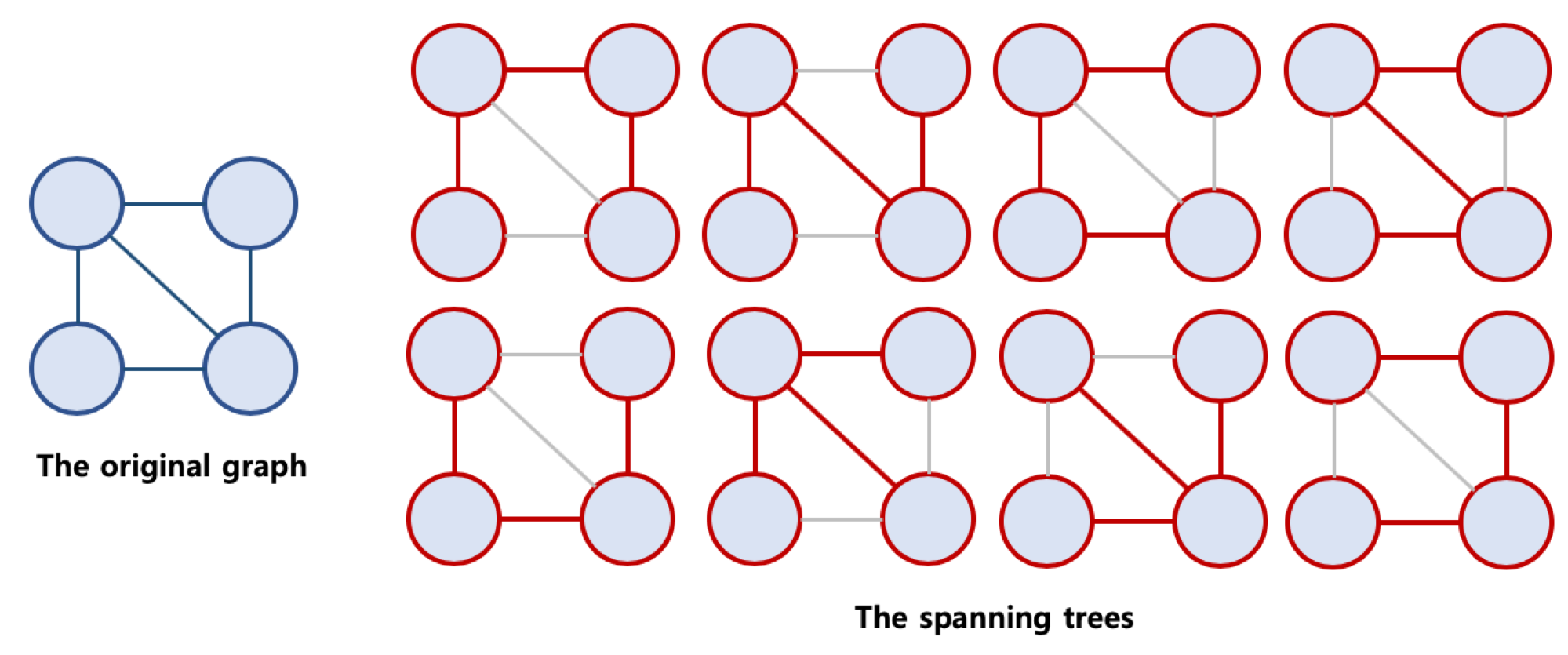
최소 신장 트리
- Minimum Spanning Tree, MST 라고 불리움
- 가능한 Spanning Tree 중에서, 간선의 가중치 합이 최소인 Spanning Tree를 지칭함
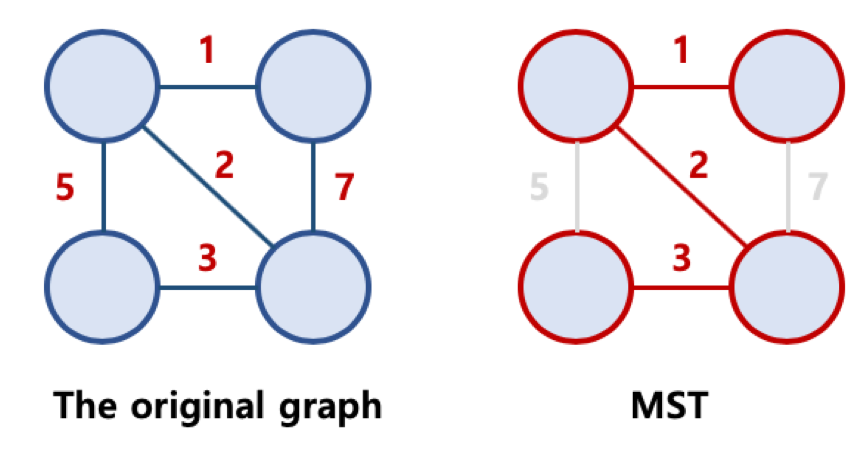
최소 신장 트리 알고리즘
- 그래프에서 최소 신장 트리를 찾을 수 있는 알고리즘이 존재함
- 대표적인 최소 신장 트리 알고리즘
- Kruskal’s algorithm (크루스칼 알고리즘), Prim’s algorithm (프림 알고리즘)
크루스칼 알고리즘 (Kruskal’s algorithm)
- 모든 정점을 독립적인 집합으로 만든다.
- 모든 간선을 비용을 기준으로 정렬하고, 비용이 작은 간선부터 양 끝의 두 정점을 비교한다.
- 두 정점의 최상위 정점을 확인하고, 서로 다를 경우 두 정점을 연결한다. (최소 신장 트리는 사이클이 없으므로, 사이클이 생기지 않도록 하는 것임)
탐욕 알고리즘을 기초로 하고 있음 (당장 눈 앞의 최소 비용을 선택해서, 결과적으로 최적의 솔루션을 찾음)
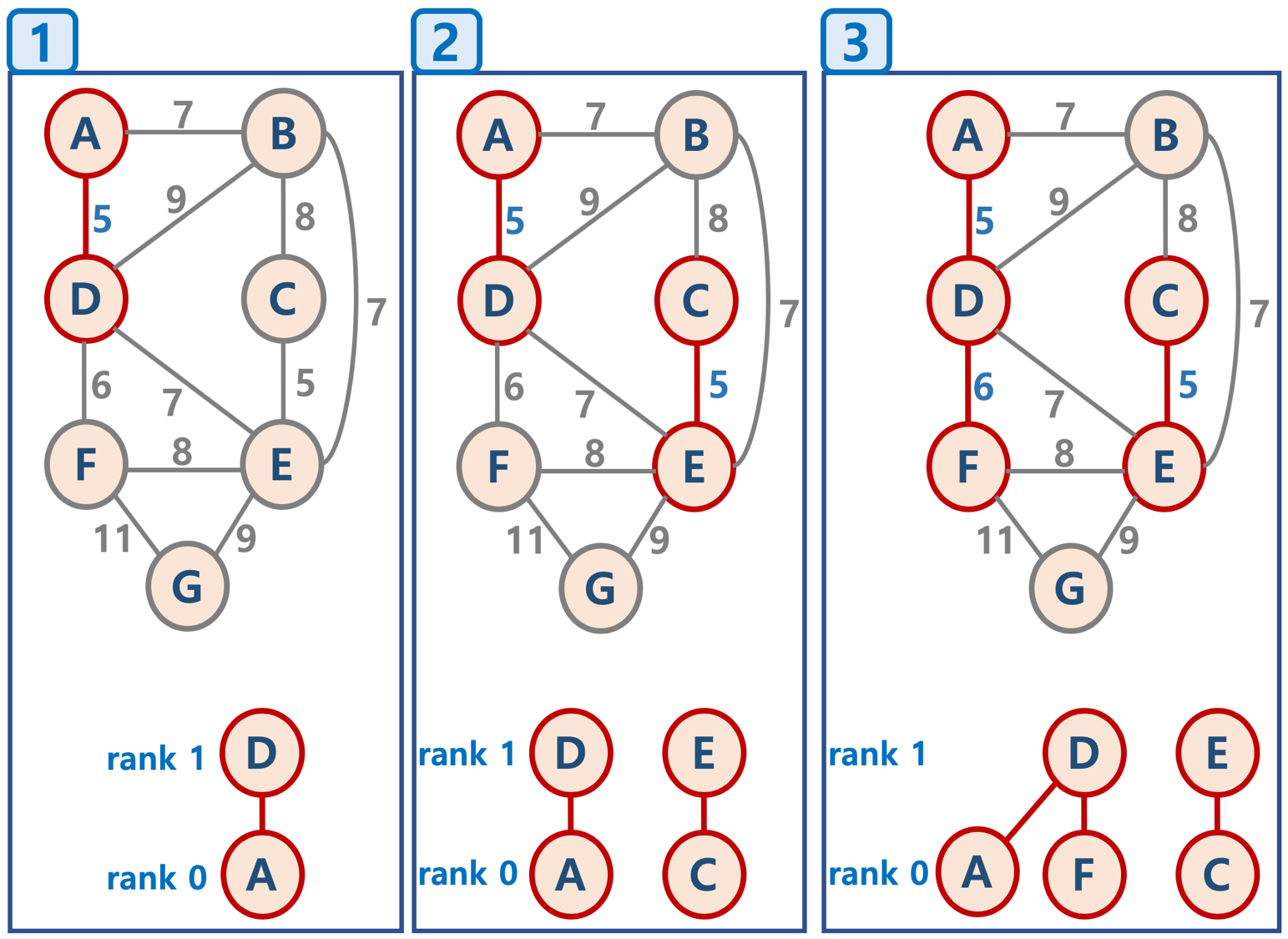
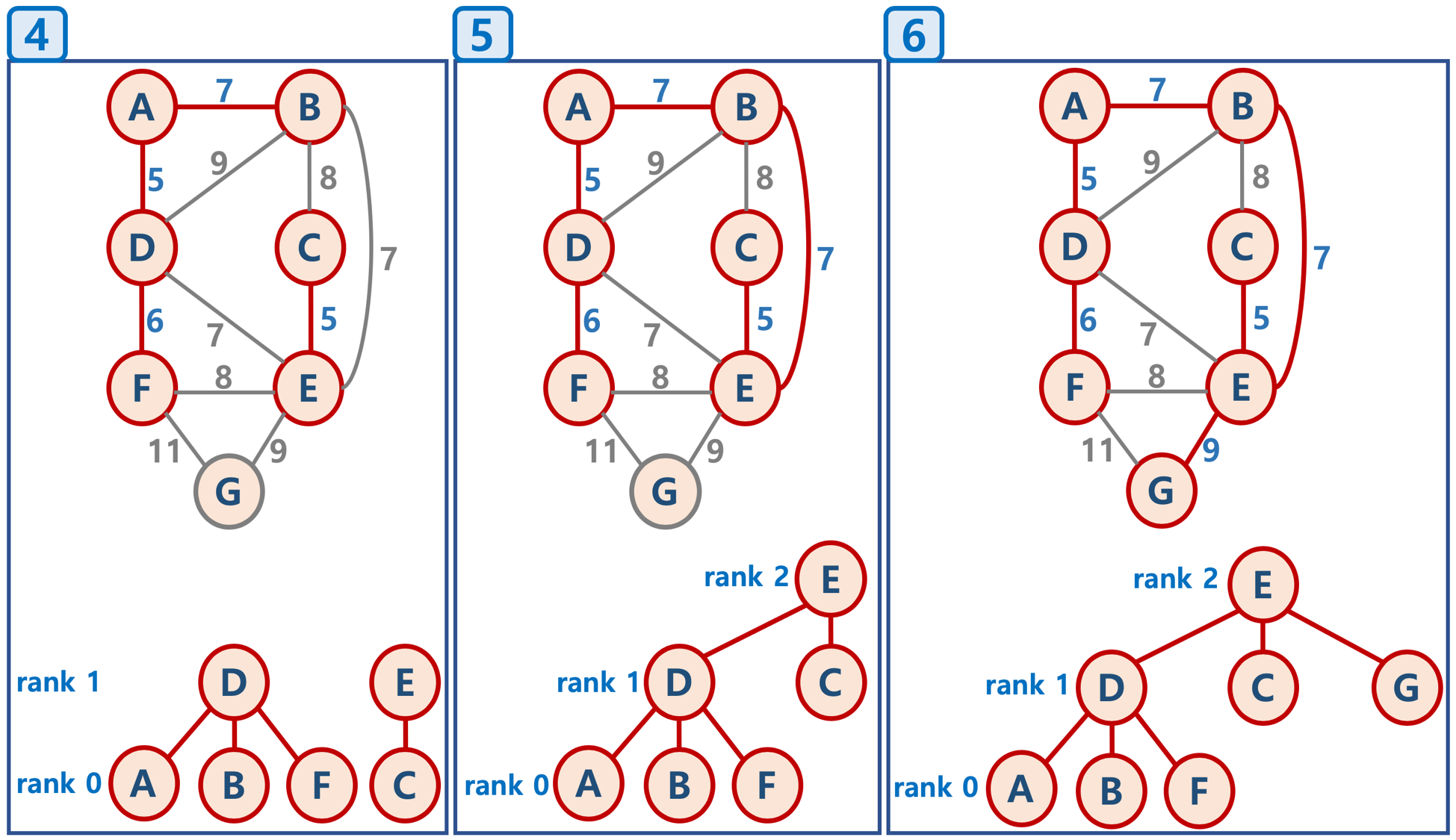
문제는 사이클이 생기느냐 안생기느냐를 어떻게 체크하냐인데 이부분을 중점으로 보자
Union-Find 알고리즘
- Disjoint Set을 표현할 때 사용하는 알고리즘으로 트리 구조를 활용하는 알고리즘
- 간단하게, 노드들 중에 연결된 노드를 찾거나, 노드들을 서로 연결할 때 (합칠 때) 사용
- Disjoint Set이란
- 서로 중복되지 않는 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료구조
- 공통 원소가 없는 (서로소) 상호 배타적인 부분 집합들로 나눠진 원소들에 대한 자료구조를 의미함
- Disjoint Set = 서로소 집합 자료구조
- 초기화
- n 개의 원소가 개별 집합으로 이뤄지도록 초기화

- n 개의 원소가 개별 집합으로 이뤄지도록 초기화
- Union
- 두 개별 집합을 하나의 집합으로 합침, 두 트리를 하나의 트리로 만듬
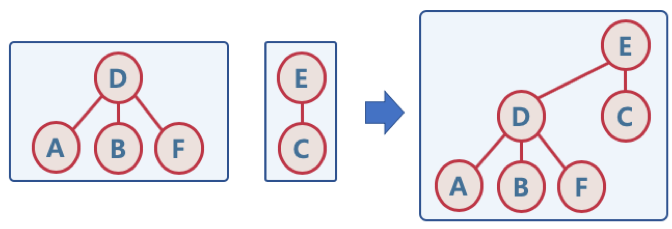
- 두 개별 집합을 하나의 집합으로 합침, 두 트리를 하나의 트리로 만듬
- Find
- 여러 노드가 존재할 때, 두 개의 노드를 선택해서, 현재 두 노드가 서로 같은 그래프에 속하는지 판별하기 위해, 각 그룹의 최상단 원소 (즉, 루트 노드)를 확인
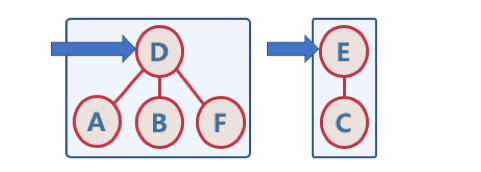
- 여러 노드가 존재할 때, 두 개의 노드를 선택해서, 현재 두 노드가 서로 같은 그래프에 속하는지 판별하기 위해, 각 그룹의 최상단 원소 (즉, 루트 노드)를 확인
Union-Find 알고리즘의 고려할 점
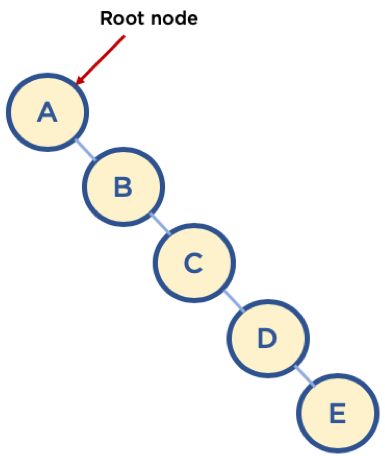
- Union 순서에 따라서, 최악의 경우 링크드 리스트와 같은 형태가 될 수 있음.
- 이 때는 Find/Union 시 계산량이 O(N) 이 될 수 있으므로, 해당 문제를 해결하기 위해, union-by-rank, path compression 기법을 사용함
union-by-rank 기법
- 각 트리에 대해 높이(rank)를 기억해 두고,
Union시 두 트리의 높이(rank)가 다르면, 높이가 작은 트리를 높이가 큰 트리에 붙임 (즉, 높이가 큰 트리의 루트 노드가 합친 집합의 루트 노드가 되게 함)
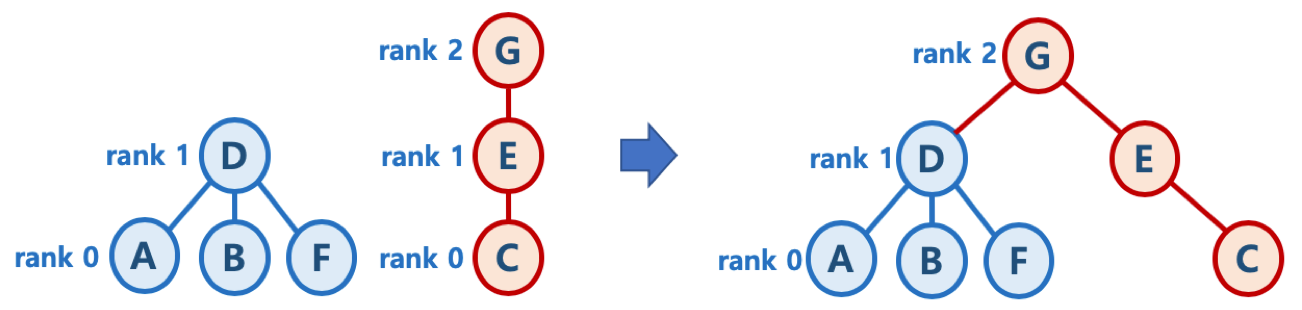
높이가 h - 1 인 두 개의 트리를 합칠 때는 한 쪽의 트리 높이를 1 증가시켜주고, 다른 쪽의 트리를 해당 트리에 붙여줌
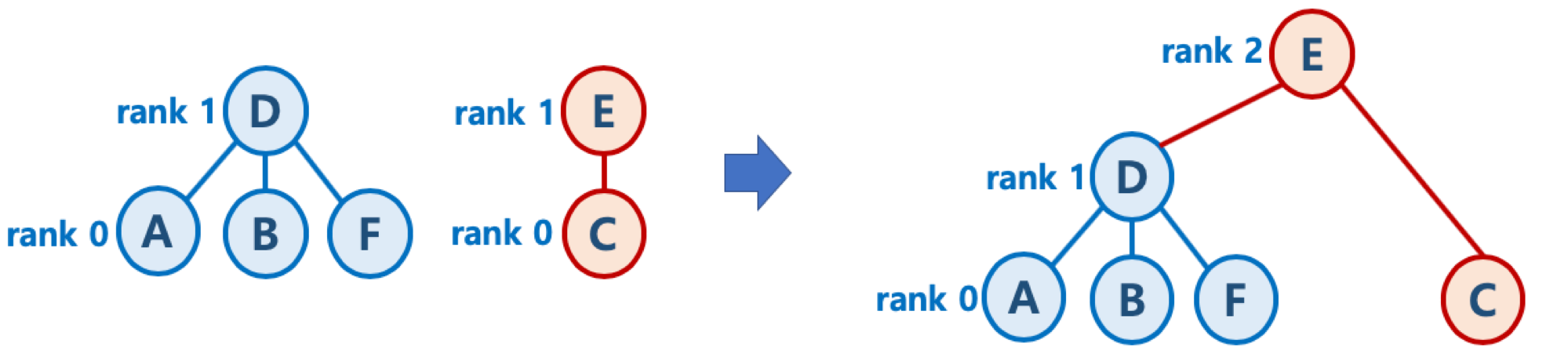
- 초기화시, 모든 원소는 높이(rank) 가 0 인 개별 집합인 상태에서, 하나씩 원소를 합칠 때, union-by-rank 기법을 사용한다면,
- 높이가 h 인 트리가 만들어지려면, 높이가 h - 1 인 두 개의 트리가 합쳐져야 함
- 높이가 h - 1 인 트리를 만들기 위해 최소 n개의 원소가 필요하다면, 높이가 h 인 트리가 만들어지기 위해서는 최소 2n개의 원소가 필요함
- 따라서 union-by-rank 기법을 사용하면, union/find 연산의 시간복잡도는 O(N) 이 아닌, $ O(log{N}) $ 로 낮출 수 있음
유니온 파인드는 부분집합을 트리로 관리한다. 유니온 연산은 하나의 집합으로 묶기위해 두개의 트리를 하나의 트리로 만든다.
그 반대편의 트리를 이 루트노드의 자식노드로 붙인다.
자세한건 뒤에 나온다.
find로직은 크루스칼 알고리즘에서는 사이클이 있냐 없냐 확인할때 쓰인다.
어차피 두 노드가 동일한 부분집합에 있으면 이건 크루스칼 알고리즘에서 싸이클이 있는지 확인하는 거.
모든 정점 연결되면 출력해준다. 그떄까지 연결된게 최소신장 트리.
크루스칼 알고리즘과 유니온파인드 알고리즘 분리. 사이클이 생기는지 확인하고 생기면 버리고 안생기면 들고가는거. 유니온으로 두 부분집합을 하나로 묶는다.
그래프에서 최소신장트리 찾을수 있는 알고리즘 = 크루스칼, 프림 알고리
크루스칼 = 모든 간선을 비용 기준으로 정렬하고 간선 비용이 작은 간선부터 사이클이 생기지 않는 한 모든 노드 연결 단 간선 끝 점 연결시 사이클 생길지 안생길지 안 생긴다면 연결 어떻게 해야할지 구현하기 위해 union find알고리즘 사용했다.
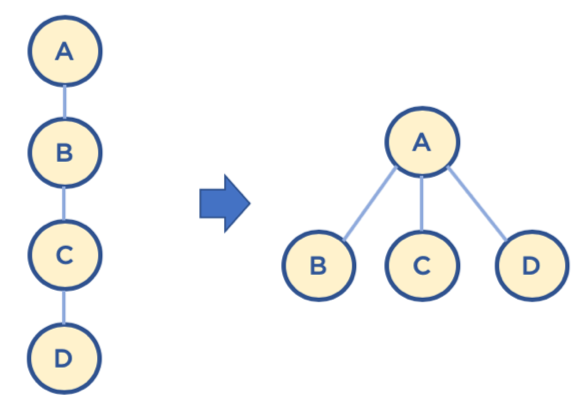
path compression
- Find를 실행한 노드에서 거쳐간 노드를 루트에 다이렉트로 연결하는 기법
- Find를 실행한 노드는 이후부터는 루트 노드를 한번에 알 수 있음
- union-by-rank 와 path compression 기법 사용시 시간 복잡도는 다음 계산식을 만족함이 증명되었음
- $ O(M log^*{N}) $
- $ log^*{N} $ 은 다음 값을 가짐이 증명되었음
- N이 $ 2^{65536} $ 값을 가지더라도, $ log^*{N} $ 의 값이 5의 값을 가지므로, 거의 O(1), 즉 상수값에 가깝다고 볼 수 있음
| N | $ log^*{N} $ |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 4 | 2 |
| 16 | 3 |
| 65536 | 4 |
| $ 2^{65536} $ | 5 |
parent = dict()
rank = dict()
def find(node):
# path compression 기법
if parent[node] != node:
parent[node] = find(parent[node])
return parent[node]
def union(node_v, node_u):
root1 = find(node_v)
root2 = find(node_u)
# union-by-rank 기법
if rank[root1] > rank[root2]:
parent[root2] = root1
else:
parent[root1] = root2
if rank[root1] == rank[root2]:
rank[root2] += 1
def make_set(node):
parent[node] = node
rank[node] = 0
def kruskal(graph):
mst = list()
# 1. 초기화
for node in graph['vertices']:
make_set(node)
# 2. 간선 weight 기반 sorting
edges = graph['edges']
edges.sort()
# 3. 간선 연결 (사이클 없는)
for edge in edges:
weight, node_v, node_u = edge
if find(node_v) != find(node_u):
union(node_v, node_u)
mst.append(edge)
return mst
7. 시간 복잡도
- 크루스컬 알고리즘의 시간 복잡도는 O(E log E)
- 다음 단계에서 2번, 간선을 비용 기준으로 정렬하는 시간에 좌우됨 (즉 간선을 비용 기준으로 정렬하는 시간이 가장 큼)
- 모든 정점을 독립적인 집합으로 만든다.
- 모든 간선을 비용을 기준으로 정렬하고, 비용이 작은 간선부터 양 끝의 두 정점을 비교한다.
- 퀵소트를 사용한다면 시간 복잡도는 O(n log n) 이며, 간선이 n 이므로 O(E log E)
- 두 정점의 최상위 정점을 확인하고, 서로 다를 경우 두 정점을 연결한다. (최소 신장 트리는 사이클이 없으므로, 사이클이 생기지 않도록 하는 것임)
- union-by-rank 와 path compression 기법 사용시 시간 복잡도가 결국 상수값에 가까움, O(1)
- 다음 단계에서 2번, 간선을 비용 기준으로 정렬하는 시간에 좌우됨 (즉 간선을 비용 기준으로 정렬하는 시간이 가장 큼)

최소 신장 트리의 이해
프림 알고리즘 (Prim’s algorithm)
- 대표적인 최소 신장 트리 알고리즘
- Kruskal’s algorithm (크루스칼 알고리즘), Prim’s algorithm (프림 알고리즘)
- 프림 알고리즘
- 시작 정점을 선택한 후, 정점에 인접한 간선중 최소 간선으로 연결된 정점을 선택하고, 해당 정점에서 다시 최소 간선으로 연결된 정점을 선택하는 방식으로 최소 신장 트리를 확장해가는 방식
- Kruskal’s algorithm 과 Prim’s algorithm 비교
- 둘다, 탐욕 알고리즘을 기초로 하고 있음 (당장 눈 앞의 최소 비용을 선택해서, 결과적으로 최적의 솔루션을 찾음)
- Kruskal’s algorithm은 가장 가중치가 작은 간선부터 선택하면서 MST를 구함
- Prim’s algorithm은 특정 정점에서 시작, 해당 정점에 연결된 가장 가중치가 작은 간선을 선택, 간선으로 연결된 정점들에 연결된 간선 중에서 가장 가중치가 작은 간선을 택하는 방식으로 MST를 구함
그림으로 이해하는 프림 알고리즘
- 임의의 정점을 선택, ‘연결된 노드 집합’에 삽입
- 선택된 정점에 연결된 간선들을 간선 리스트에 삽입
- 간선 리스트에서 최소 가중치를 가지는 간선부터 추출해서,
- 해당 간선에 연결된 인접 정점이 ‘연결된 노드 집합’에 이미 들어 있다면, 스킵함(cycle 발생을 막기 위함)
- 해당 간선에 연결된 인접 정점이 ‘연결된 노드 집합’에 들어 있지 않으면, 해당 간선을 선택하고, 해당 간선 정보를 ‘최소 신장 트리’에 삽입
- 추출한 간선은 간선 리스트에서 제거
- 간선 리스트에 더 이상의 간선이 없을 때까지 3-4번을 반복
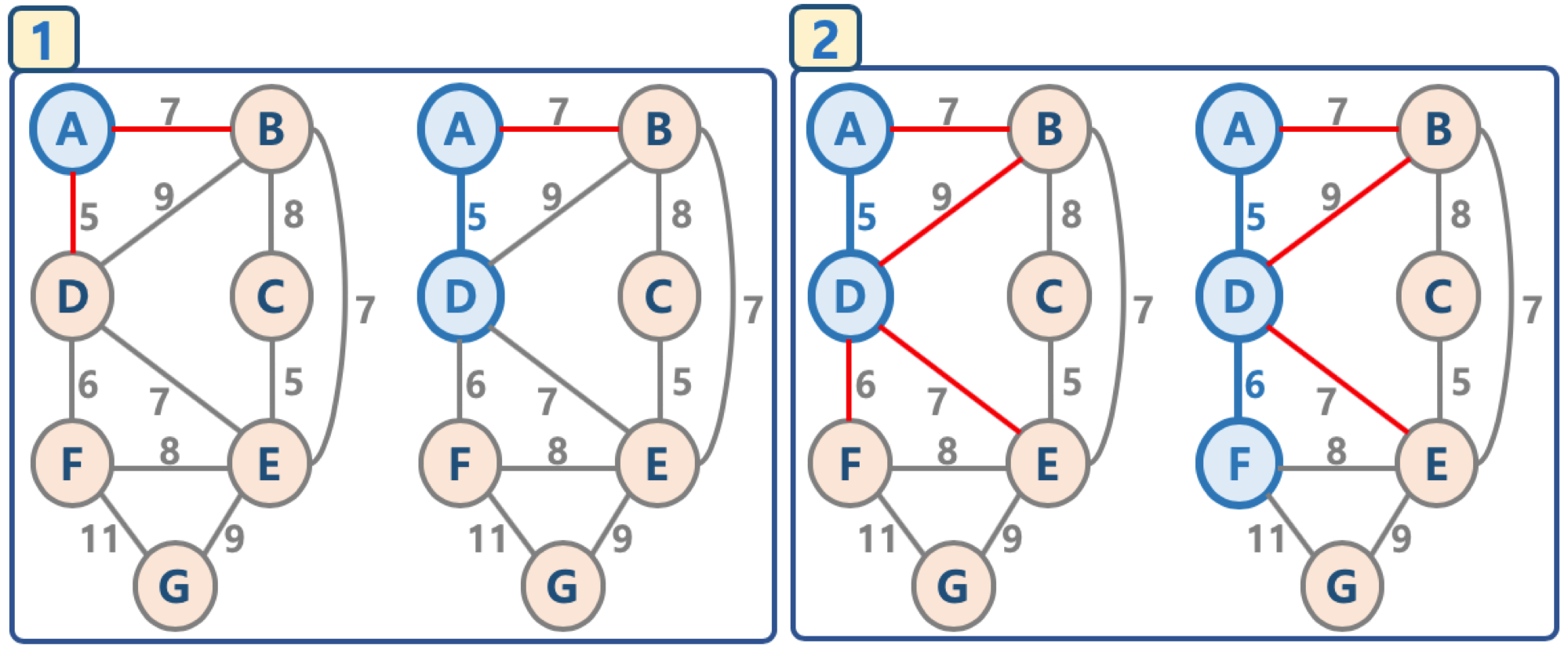
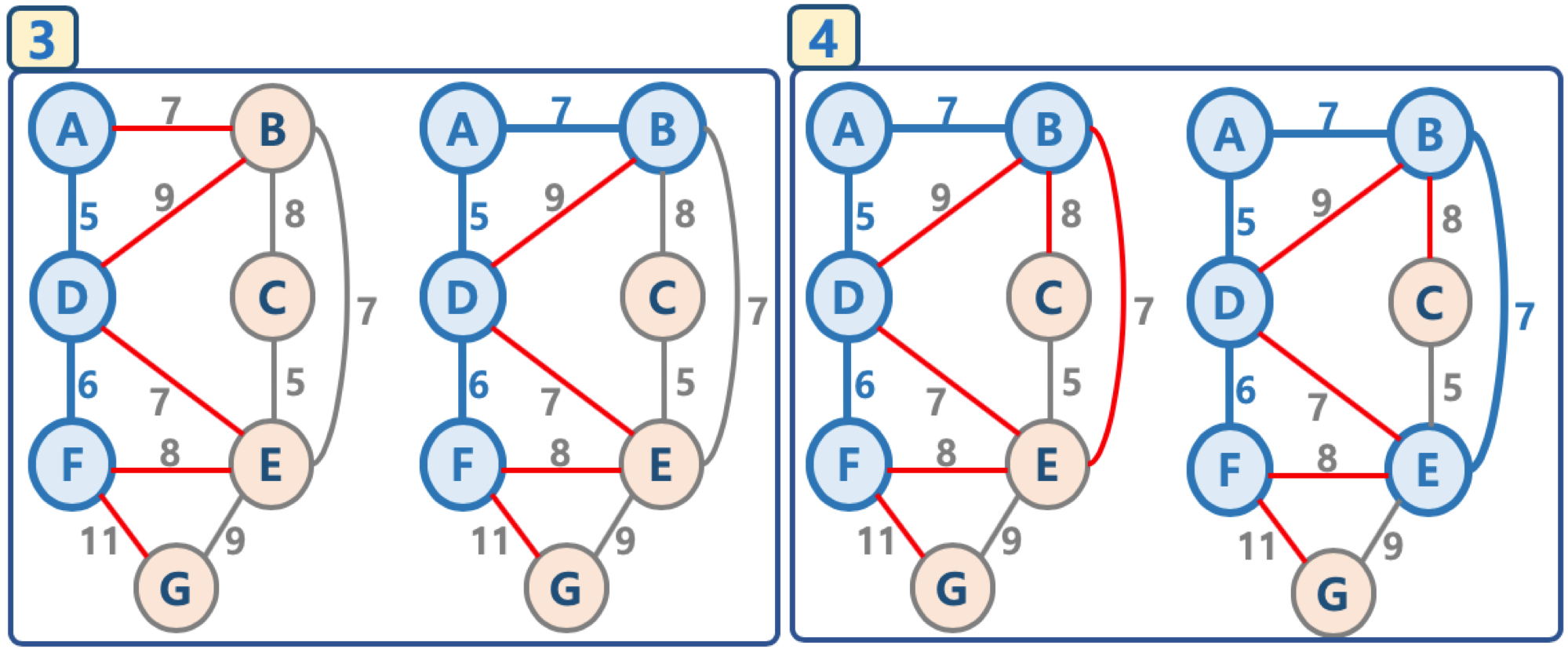
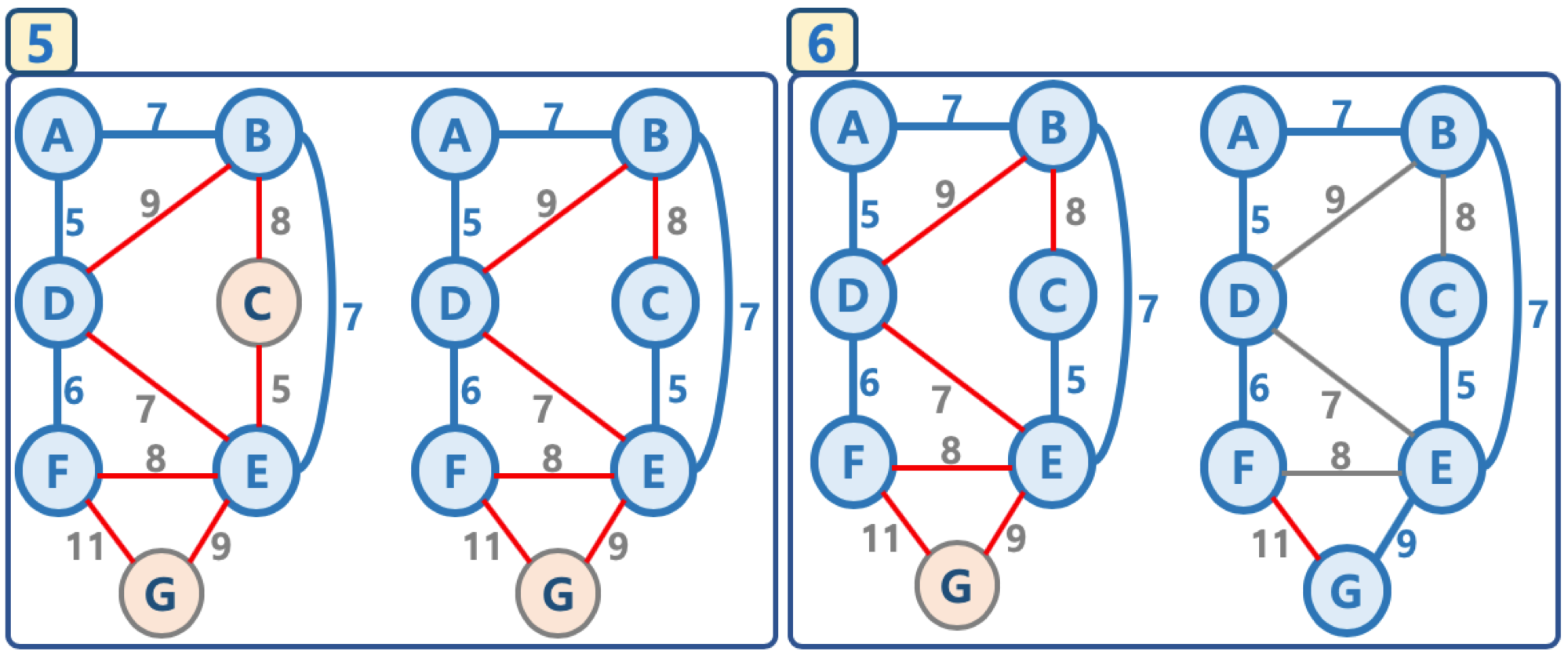
### 프림 알고리즘 파이썬 코드
0. 모든 간선 정보를 저장 (**adjacent_edges**)
1. 임의의 정점을 선택, '연결된 노드 집합(**connected_nodes**)'에 삽입
2. 선택된 정점에 연결된 간선들을 간선 리스트(**candidate_edge_list**)에 삽입
3. 간선 리스트(**candidate_edge_list**)에서 최소 가중치를 가지는 간선부터 추출해서,
- 해당 간선에 연결된 인접 정점이 '연결된 노드 집합'에 이미 들어 있다면, 스킵함(cycle 발생을 막기 위함)
- 해당 간선에 연결된 인접 정점이 '연결된 노드 집합'에 들어 있지 않으면, 해당 간선을 선택하고, 해당 간선 정보를 '최소 신장 트리(**mst**)'에 삽입
- 해당 간선에 연결된 인접 정점의 간선들 중, '연결된 노드 집합(**connected_nodes**)' 에 없는 노드와 연결된 간선들만 간선 리스트(**candidate_edge_list**) 에 삽입
- '연결된 노드 집합(**connected_nodes**)' 에 있는 노드와 연결된 간선들을 간선 리스트에 삽입해도, 해당 간선은 스킵될 것이기 때문임
- 어차피 스킵될 간선을 간선 리스트(**candidate_edge_list**)에 넣지 않으므로 해서, 간선 리스트(**candidate_edge_list**)에서 최소 가중치를 가지는 간선부터 추출하기 위한 자료구조 유지를 위한 effort를 줄일 수 있음 (예, 최소힙 구조 사용)
4. 선택된 간선은 간선 리스트에서 제거
5. 간선 리스트에 더 이상의 간선이 없을 때까지 3-4번을 반복
from collections import defaultdict
from heapq import *
def prim(start_node, edges):
mst = list()
adjacent_edges = defaultdict(list)
for weight, n1, n2 in edges:
adjacent_edges[n1].append((weight, n1, n2))
adjacent_edges[n2].append((weight, n2, n1))
connected_nodes = set(start_node)
candidate_edge_list = adjacent_edges[start_node]
heapify(candidate_edge_list)
while candidate_edge_list:
weight, n1, n2 = heappop(candidate_edge_list)
if n2 not in connected_nodes:
connected_nodes.add(n2)
mst.append((weight, n1, n2))
for edge in adjacent_edges[n2]:
if edge[2] not in connected_nodes:
heappush(candidate_edge_list, edge)
return mst
시간 복잡도
- 최악의 경우, while 구문에서 모든 간선에 대해 반복하고, 최소 힙 구조를 사용하므로 O($ElogE$) 시간 복잡도를 가짐
참고: 개선된 프림 알고리즘
- 간선이 아닌 노드를 중심으로 우선순위 큐를 적용하는 방식(시간 복잡도가 향상된다(더 빨라진다).)
- 초기화 - 정점:key 구조를 만들어놓고, 특정 정점의 key값은 0, 이외의 정점들의 key값은 무한대로 놓음. 모든 정점:key 값은 우선순위 큐에 넣음
- 가장 key값이 적은 정점:key를 추출한 후(pop 하므로 해당 정점:key 정보는 우선순위 큐에서 삭제됨), (extract min 로직이라고 부름)
- 해당 정점의 인접한 정점들에 대해 key 값과 연결된 가중치 값을 비교하여 key값이 작으면 해당 정점:key 값을 갱신
- 정점:key 값 갱신시, 우선순위 큐는 최소 key값을 가지는 정점:key 를 루트노드로 올려놓도록 재구성함 (decrease key 로직이라고 부름)
- 개선된 프림 알고리즘 구현시 고려 사항
- 우선순위 큐(최소힙) 구조에서, 이미 들어가 있는 데이터의 값 변경시, 최소값을 가지는 데이터를 루트노드로 올려놓도록 재구성하는 기능이 필요함
- 구현 복잡도를 줄이기 위해, heapdict 라이브러리를 통해, 해당 기능을 간단히 구현
from heapdict import heapdict #heapdict으로 이 안이 최소데이터가 pop되면 우선순위가 루트노드에 올려지도록 최소힙의 형태를 지니고 그안에 존재한 노드 바꿀때 최소값을 바꾸는걸 가지고 있다.(구현 복잡도 확 줄임)
def prim(graph, start):
mst, keys, pi, total_weight = list(), heapdict(), dict(), 0
#최소 간선리스트 저장하는 변수 mst라 만들어놓고
#노드와 키값을 가진 최소 힙구조 만들어야 되서 heapdict을 써서 keys만들고 pi는 아까 키값 업데이트 시 어느노드에서 들어와서 업데이트 됐는지 하기위해 pi라 주고 이 키값은 a로부터 가중치가 업데이트 됐구나 이런식
for node in graph.keys():
keys[node] = float('inf')
pi[node] = None
keys[start], pi[start] = 0, start
while keys:
current_node, current_key = keys.popitem()
mst.append([pi[current_node], current_node, current_key])
total_weight += current_key
for adjacent, weight in mygraph[current_node].items():
if adjacent in keys and weight < keys[adjacent]:
keys[adjacent] = weight
pi[adjacent] = current_node
return mst, total_weight
개선된 프림 알고리즘의 시간 복잡도: $ O(ElogV) $
최초 key 생성 시간 복잡도: $ O(V) $ (노드개수만큼 반복)
- while 구문과 keys.popitem() 의 시간 복잡도는 $ O(VlogV) $
- while 구문은 V(노드 갯수) 번 실행됨
- heap 에서 최소 key 값을 가지는 노드 정보 추출 시(pop)의 시간 복잡도: $ O(logV) $
- for 구문의 총 시간 복잡도는 $ O(ElogV) $(간선이 체크 될때마다 key값이 업데이트 되서 재구성 됨.)
- for 구문은 while 구문 반복시에 결과적으로 총 최대 간선의 수 E만큼 실행 가능 $ O(E) $
- for 구문 안에서 key값 변경시마다 heap 구조를 변경해야 하며, heap 에는 최대 V 개의 정보가 있으므로 $ O(logV) $
일반적인 heap 자료 구조 자체에는 본래 heap 내부의 데이터 우선순위 변경시, 최소 우선순위 데이터를 루트노드로 만들어주는 로직은 없음. 이를 decrease key 로직이라고 부름, 해당 로직은 heapdict 라이브러리를 활용해서 간단히 적용가능
- 따라서 총 시간 복잡도는 $ O(V + VlogV + ElogV) $ 이며,
- O(V)는 전체 시간 복잡도에 큰 영향을 미치지 않으므로 삭제,
- E > V 이므로 (최대 $ V^2 = E $ 가 될 수 있음), $ O((V + E)logV) $ 는 간단하게 $ O(ElogV) $ 로 나타낼 수 있음
프림알고리즘은 간단히 정리하면
크루스칼 알고리즘은 모든 간에서 간선을 대상으로 해서 가장 weight가 적은 알고리즘 연결하기 시작.
프림 알고리즘은 지금 연결된 노드의 붙어있는 간선중에서 weight가 작은 간을 이를 최소신장트리에 연결.
기본적인 컨셉과 개선된 알고리즘은 노드 개수 중심으로 돈다.
기본적인 컨셉은 간선을 중심으로 돌지만
개선된 알고리즘은 노드를 중심으로 돈다(노드가 간선보다 작으므로)
노드마다 키값 매겨서 가장 작은 키값 선택하고 그걸 업데이트 한걸 최소신장트리에 넣는다.
엄청 깊게 할 필요는 없지만 여기까지 다하면 프림알고리즘은 완벽하게 다 한거.