[python] python Data Structure
배열(Array), List(Python)
1. 배열은 왜 필요할까?
- 같은 종류의 데이터를 효율적으로 관리하기 위해 사용
- 같은 종류의 데이터를 순차적으로 저장
- 장점:
- 빠른 접근 가능
- 첫 데이터의 위치에서 상대적인 위치로 데이터 접근(인덱스 번호로 접근)
- 빠른 접근 가능
단점:
- 데이터 추가/삭제의 어려움
- 미리 최대 길이를 지정해야 함
- 데이터 추가/삭제의 어려움
파이썬에서는 리스트로 배열 구현 가능
- range(stop): range(10)은 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
- range(start, stop): range(1, 11)은 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
- range(start, stop, step): range(0, 20, 2)은 0, 2, 4, 6, 8, 10, 12, 14, 16, 18
- start, stop, step은 음수로 지정 가능
큐(Queue)
- 줄을 서는 행위와 유사
- 가장 먼저 넣은 데이터를 가장 먼저 꺼낼 수 있는 구조
- 음식점에서 가장 먼저 줄을 선 사람이 제일 먼저 음식점에 입장하는 것과 동일
- FIFO(First-In, First-Out) 또는 LILO(Last-In, Last-Out) 방식으로 스택과 꺼내는 순서가 반대

출처: http://www.stoimen.com/blog/2012/06/05/computer-algorithms-stack-and-queue-data-structure/
- Enqueue: 큐에 데이터를 넣는 기능
- Dequeue: 큐에서 데이터를 꺼내는 기능
- https://visualgo.net/en/list
어디에 큐가 많이 쓰일까?
- 멀티 태스킹을 위한 프로세스 스케쥴링 방식을 구현하기 위해 많이 사용됨 (운영체제 참조)
이건 알아두고 가야 한다.
큐의 경우에는 장단점 보다는 (특별히 언급되는 장단점이 없음), 큐의 활용 예로 프로세스 스케쥴링 방식을 함께 이해해두는 것이 좋음
스택(Stack)
- 데이터를 제한적으로 접근할 수 있는 구조
- 한쪽 끝에서만 자료를 넣거나 뺄 수 있는 구조
- 가장 나중에 쌓은 데이터를 가장 먼저 빼낼 수 있는 데이터 구조
- 큐: FIFO 정책
- 스택: LIFO 정책
스택 구조
스택은 LIFO(Last In, Fisrt Out) 또는 FILO(First In, Last Out) 데이터 관리 방식을 따름
- LIFO: 마지막에 넣은 데이터를 가장 먼저 추출하는 데이터 관리 정책
- FILO: 처음에 넣은 데이터를 가장 마지막에 추출하는 데이터 관리 정책
대표적인 스택의 활용
- 컴퓨터 내부의 프로세스 구조의 함수 동작 방식
주요 기능
- push(): 데이터를 스택에 넣기
- pop(): 데이터를 스택에서 꺼내기
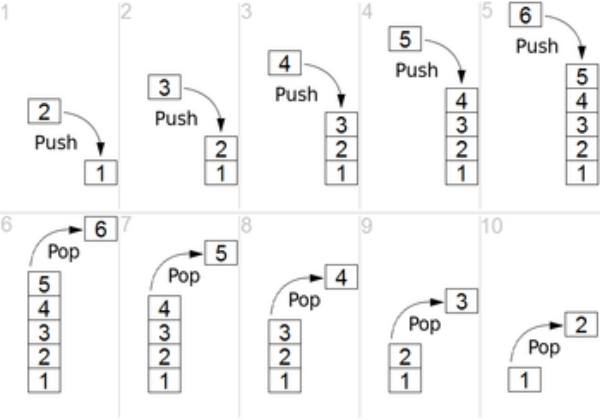
스택 구조와 프로세스 스택
- 스택 구조는 프로세스 실행 구조의 가장 기본
- 함수 호출시 프로세스 실행 구조를 스택과 비교해서 이해 필요
자료 구조 스택의 장단점
- 장점
- 구조가 단순해서, 구현이 쉽다.
- 데이터 저장/읽기 속도가 빠르다.
- 단점 (일반적인 스택 구현시)
- 데이터 최대 갯수를 미리 정해야 한다.
- 파이썬의 경우 재귀 함수는 1000번까지만 호출이 가능함
- 저장 공간의 낭비가 발생할 수 있음
- 미리 최대 갯수만큼 저장 공간을 확보해야 함
- 데이터 최대 갯수를 미리 정해야 한다.
스택은 단순하고 빠른 성능을 위해 사용되므로, 보통 배열 구조를 활용해서 구현하는 것이 일반적임. 이 경우, 위에서 열거한 단점이 있을 수 있음
링크드 리스트(Linked List)
- 연결 리스트라고도 함
- 배열은 순차적으로 연결된 공간에 데이터를 나열하는 데이터 구조(배열 문제 해결하기 위해 나온게 링크드 리스트. 배열은 미리 특정한 연결된 공간을 예약하고 데이터를 쓰고있는 구조, 링크드 리스트는 미리 예약 안하고 필요할 때마다 데이터를 더 추가하는 구조이다. )
- 링크드 리스트는 떨어진 곳에 존재하는 데이터를 화살표로 연결해서 관리하는 데이터 구조
- 본래 C언어에서는 주요한 데이터 구조이지만, 파이썬은 리스트 타입이 링크드 리스트의 기능을 모두 지원
- 링크드 리스트 기본 구조와 용어
- 노드(Node): 데이터 저장 단위 (데이터값, 포인터) 로 구성
- 포인터(pointer): 각 노드 안에서, 다음이나 이전의 노드와의 연결 정보를 가지고 있는 공간
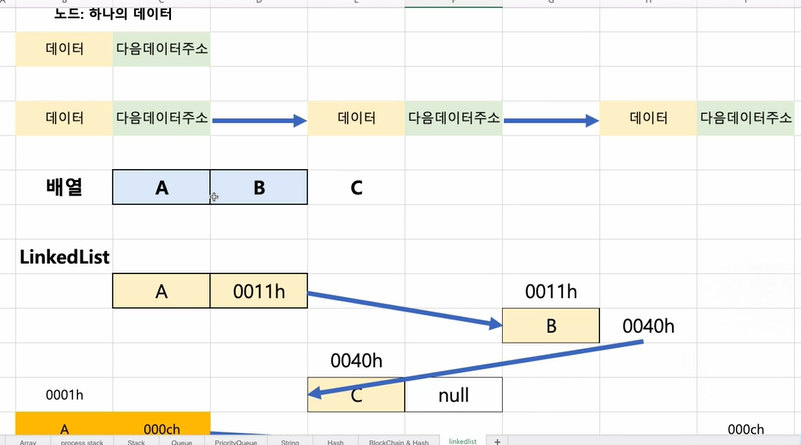
- 일반적인 링크드 리스트 형태
 (출처: wikipedia, https://en.wikipedia.org/wiki/Linked_list)
(출처: wikipedia, https://en.wikipedia.org/wiki/Linked_list)
Node 구현
- 보통 파이썬에서 링크드 리스트 구현시, 파이썬 클래스를 활용함
- 파이썬 객체지향 문법 이해 필요
배열과 링크드 리스트 차이
배열은 만약 그림처럼 A,B를 가진 배열에 C를 넣을 수가 없다.(A,B가 가지고 있기 떄문. 파이썬은 append이든 뭐든 될지 몰라도 만약 C나 자바처럼 배열크기가 정해지면 범위를 초과해서 넣을 수가 없다.)
링크드리스트는 어느 공간이던 노드 저장할 공간 만들고 그 앞에 새로운 데이터를 넣고 앞의 데이터가 새로생성된 노드를 가리키도록 주소가 가리키게만 만들면 된다.
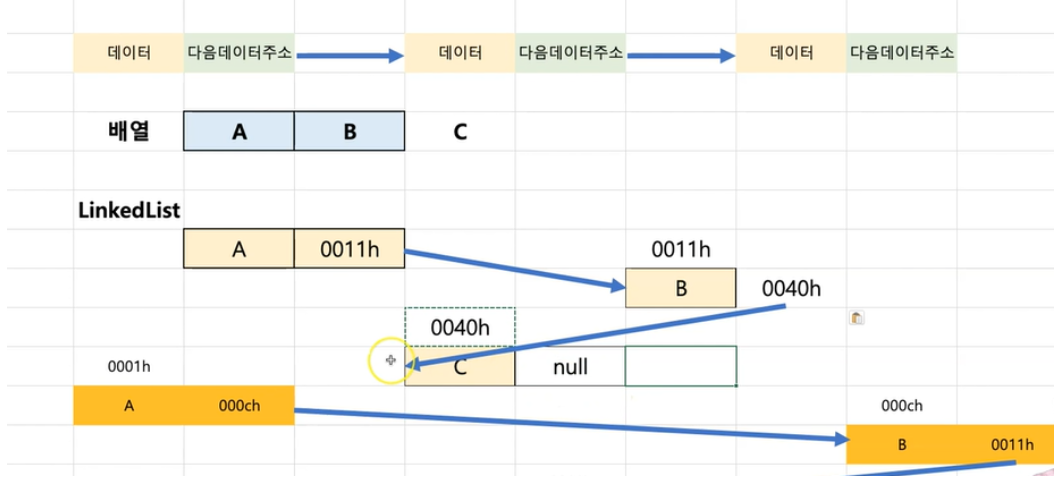
링크드 리스트는 이런 구조라 무한정으로 뻗어나갈 수 가있다.
링크드 리스트의 장단점 (전통적인 C언어에서의 배열과 링크드 리스트)
- 장점
- 미리 데이터 공간을 미리 할당하지 않아도 됨
- 배열은 미리 데이터 공간을 할당 해야 함
- 미리 데이터 공간을 미리 할당하지 않아도 됨
- 단점
- 연결을 위한 별도 데이터 공간이 필요하므로, 저장공간 효율이 높지 않음
- 연결 정보를 찾는 시간이 필요하므로 접근 속도가 느림
- 중간 데이터 삭제시, 앞뒤 데이터의 연결을 재구성해야 하는 부가적인 작업 필요
링크드 리스트의 복잡한 기능1 (링크드 리스트 데이터 사이에 데이터를 추가)
- 링크드 리스트는 유지 관리에 부가적인 구현이 필요함
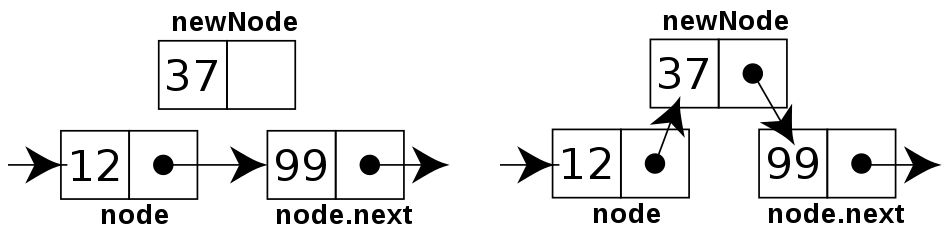
(출처: wikipedia, https://en.wikipedia.org/wiki/Linked_list)
링크드 리스트의 복잡한 기능2 (특정 노드를 삭제)
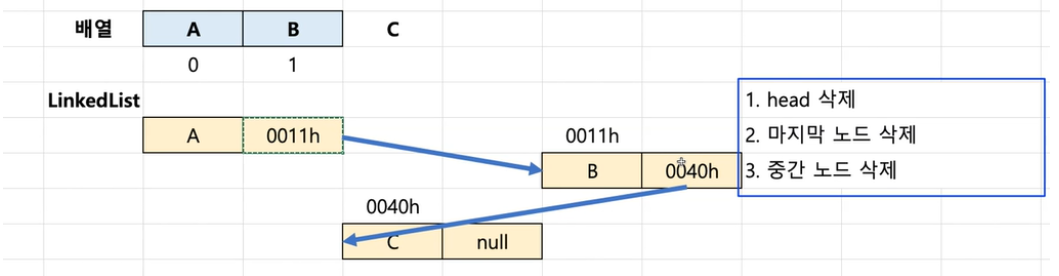
링크드 리스트는 맨앞 노드를 꼭 가져야 하고 그걸 헤드라 하기로 했다. 삭제하려면 헤드가 다음 노드로 바뀌어야 한다 C라는 거 삭제하려면(맨 마지막 노드) 그냥 없애면 되지만 그 앞의 노드의 주소값을 null, 또는 none으로 바꿔줘야 한다.
중간노드삭제는 B를 없애고 C로 A의 노드 주소값을 바꿔줘야한다.
- 다음 코드는 위의 코드에서 delete 메서드만 추가한 것이므로 해당 메서드만 확인하면 됨
다양한 링크드 리스트 구조
더블 링크드 리스트(Doubly linked list) 기본 구조
- 이중 연결 리스트라고도 함
장점: 양방향으로 연결되어 있어서 노드 탐색이 양쪽으로 모두 가능
 (출처: wikipedia, https://en.wikipedia.org/wiki/Linked_list)
(출처: wikipedia, https://en.wikipedia.org/wiki/Linked_list)
노드 찾고 연결할떄 반드 노드가 3개라 가정시 마지막 데이터든 어느곳이든 반드시 헤드데이터 찾고 원하는 데이터로 이동해야 한다.
노드가 1만개라 생각해보자 맨 끝에 있으면 1만번을 검색해야한다.
이 만개의 노드가 0~9999까지 있다 가정시 8000번대에 있다 가정하고 소트정렬 하면 8천번인데 8000이 끝에서 가까우니까 8000번은 2000번 정도만 하면 가능하다.
찾고자 하는 위치에 따라 앞에서 검색해서 찾든 뒤에서부터 검색해서 찾든 찾는 곳의 위치를 알수 있고 이렇게 적용해서 찾고 싶다 -> 그래서 나온게 LinkedList다.
더블 링크드 리스트는 노드의 구조가 좀 다르다.
기존의 일반 링크드리스트의 구조는 데이터와 다음 노드 가리키는 주소 갖는 반면에 더블 링크드리스트는 그 앞의 구조를 저장할수 있게 만든다.
앞의 구조를 갖게 되면 맨끝에서 앞으로 , 또는 반대로 맨 뒤에서 맨 앞으로 찾아갈 수도 있다.
기존의 링크드리스트 관점인 앞에서부터 검색해야된다는 점을 보완한 점이 더블 링크드 리스트이다.
노드는 앞뒤로 주소 갖고 있다.
시간복잡도
알고리즘 복잡도 표현 방법
알고리즘 복잡도 계산이 필요한 이유
하나의 문제를 푸는 알고리즘은 다양할 수 있음
- 정수의 절대값 구하기
- 1, -1 -» 1
- 방법1: 정수값을 제곱한 값에 다시 루트를 씌우기
- 방법2: 정수가 음수인지 확인해서, 음수일 때만, -1을 곱하기
다양한 알고리즘 중 어느 알고리즘이 더 좋은지를 분석하기 위해, 복잡도를 정의하고 계산함
알고리즘 복잡도 계산 항목
- 시간 복잡도: 알고리즘 실행 속도
- 공간 복잡도: 알고리즘이 사용하는 메모리 사이즈
가장 중요한 시간 복잡도를 꼭 이해하고 계산할 수 있어야 함
-> 시간복잡도는 반복문이 가장 큰 영향을 끼친다. 입력이 커질수록 반복문이 알고리즘 수행시간에 큰 영향을 끼친다.
알고리즘 성능 표기법
Big O (빅-오) 표기법: O(N)
- 알고리즘 최악의 실행 시간을 표기
- 가장 많이/일반적으로 사용함
- 아무리 최악의 상황이라도, 이정도의 성능은 보장한다는 의미이기 때문
Ω (오메가) 표기법: Ω(N)
- 오메가 표기법은 알고리즘 최상의 실행 시간을 표기
Θ (세타) 표기법: Θ(N)
- 오메가 표기법은 알고리즘 평균 실행 시간을 표기
시간 복잡도 계산은 반복문이 핵심 요소임을 인지하고, 계산 표기는 최상, 평균, 최악 중, 최악의 시간인 Big-O 표기법을 중심으로 익히면 됨
대문자 O 표기법
- 빅 오 표기법, Big-O 표기법 이라고도 부름
O(입력)
- 입력 n 에 따라 결정되는 시간 복잡도 함수
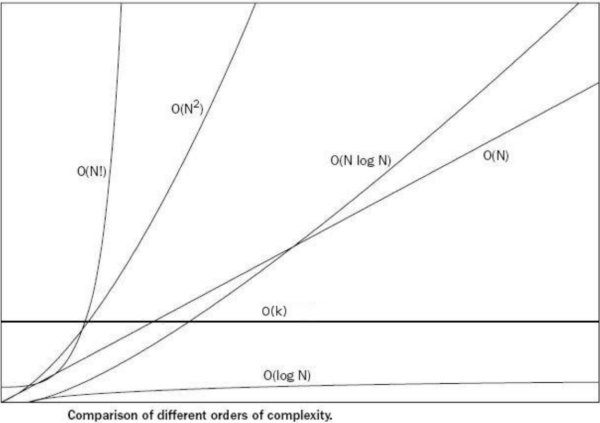
- O(1), O($log n$), O(n), O(n$log n$), O($n^2$), O($2^n$), O(n!)등으로 표기함
- 입력 n 의 크기에 따라 기하급수적으로 시간 복잡도가 늘어날 수 있음
- O(1) < O($log n$) < O(n) < O(n$log n$) < O($n^2$) < O($2^n$) < O(n!)
- 참고: log n 의 베이스는 2 - $log_2 n$
- O(1) < O($log n$) < O(n) < O(n$log n$) < O($n^2$) < O($2^n$) < O(n!)
- 단순하게 입력 n에 따라, 몇번 실행이 되는지를 계산하면 됩니다.
- 표현식에 가장 큰 영향을 미치는 n 의 단위로 표기합니다.
- n이 1이든 100이든, 1000이든, 10000이든 실행을
- 무조건 2회(상수회) 실행한다: O(1)
if n > 10: print(n) - n에 따라, n번, n + 10 번, 또는 3n + 10 번등 실행한다: O(n)
variable = 1 for num in range(3): for index in range(n): print(index) - n에 따라, $n^2$번, $n^2$ + 1000 번, 100$n^2$ - 100, 또는 300$n^2$ + 1번등 실행한다: O($n^2$)
variable = 1 for i in range(300): for num in range(n): for index in range(n): print(index)
- 무조건 2회(상수회) 실행한다: O(1)
- 빅 오 입력값 표기 방법
- 예:
- 만약 시간 복잡도 함수가 2$n^2$ + 3n 이라면
- 가장 높은 차수는 2$n^2$
- 상수는 실제 큰 영향이 없음
- 결국 빅 오 표기법으로는 O($n^2$) (서울부터 부산까지 가는 자동차의 예를 상기)
- 만약 시간 복잡도 함수가 2$n^2$ + 3n 이라면
- 예:
해쉬테이블(Hash Table)
해쉬 구조
- Hash Table: 키(Key)에 데이터(Value)를 저장하는 데이터 구조
- Key를 통해 바로 데이터를 받아올 수 있으므로, 속도가 획기적으로 빨라짐
- 파이썬 딕셔너리(Dictionary) 타입이 해쉬 테이블의 예: Key를 가지고 바로 데이터(Value)를 꺼냄
- 보통 배열로 미리 Hash Table 사이즈만큼 생성 후에 사용 (공간과 탐색 시간을 맞바꾸는 기법)
- 단, 파이썬에서는 해쉬를 별도 구현할 이유가 없음 - 딕셔너리 타입을 사용하면 됨
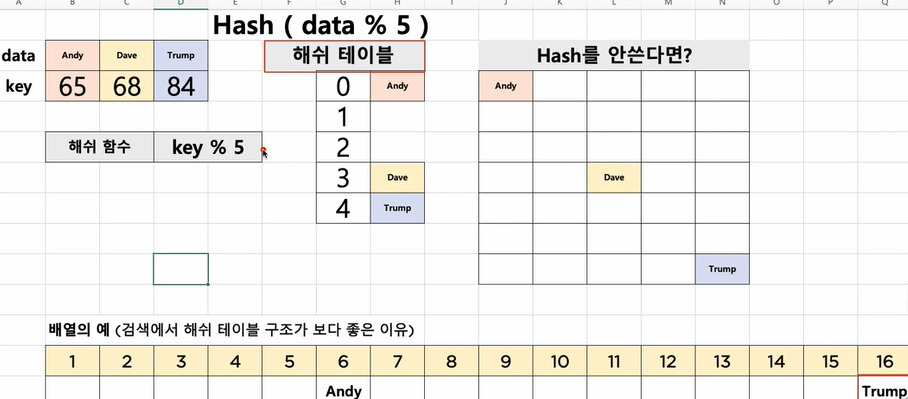
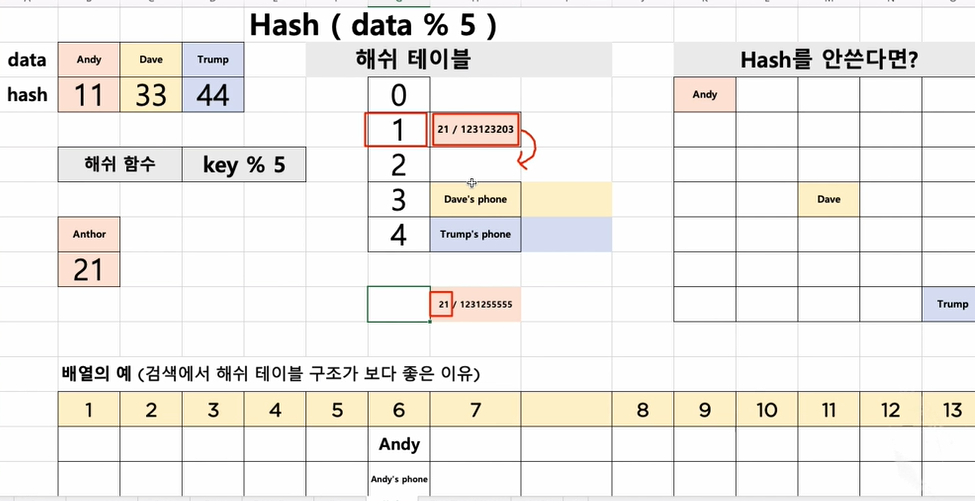
배열과 차이는 배열은 인덱스 위치 한거 하나하나 찾아야 하지만(16번) 해쉬 테이블은 이 트럼프라는 데이터가 어디있는지 알수 있어 곧바로 데이터를 찾아올 수 있다.
key를 해쉬함수에 넣으면 데이터가 저장되있는 위치가 나온다.
배열을 다 검색할 필요없이 데이터가 저장된 위치를 알아낼 수 있다. 그런 구조를 해쉬테이블 구조라 한다.
파이썬에서도 딕셔너리를 쓰는데 이게 해쉬함수를 이용한 자료구조이다.
관련 용어
- 해쉬(Hash): 임의 값을 고정 길이로 변환하는 것
- 해쉬 테이블(Hash Table): 키 값의 연산에 의해 직접 접근이 가능한 데이터 구조
- 해싱 함수(Hashing Function): Key에 대해 산술 연산을 이용해 데이터 위치를 찾을 수 있는 함수
- 해쉬 값(Hash Value) 또는 해쉬 주소(Hash Address): Key를 해싱 함수로 연산해서, 해쉬 값을 알아내고, 이를 기반으로 해쉬 테이블에서 해당 Key에 대한 데이터 위치를 일관성있게 찾을 수 있음
- 슬롯(Slot): 한 개의 데이터를 저장할 수 있는 공간
- 저장할 데이터에 대해 Key를 추출할 수 있는 별도 함수도 존재할 수 있음
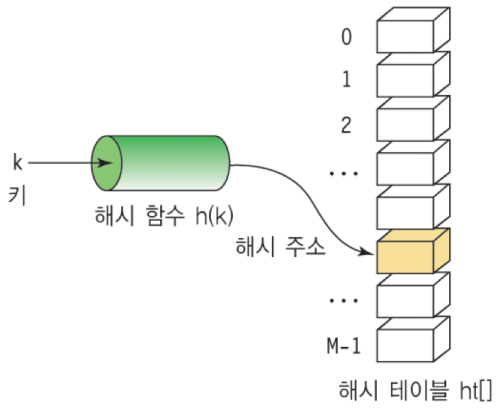
키에 해시함수를 넣으면 특별한 주소가 나오는데 이 주소와 데이터 공간이 연결되어있다. 이 구조를 해시테이블이라 한다.
다시 보면
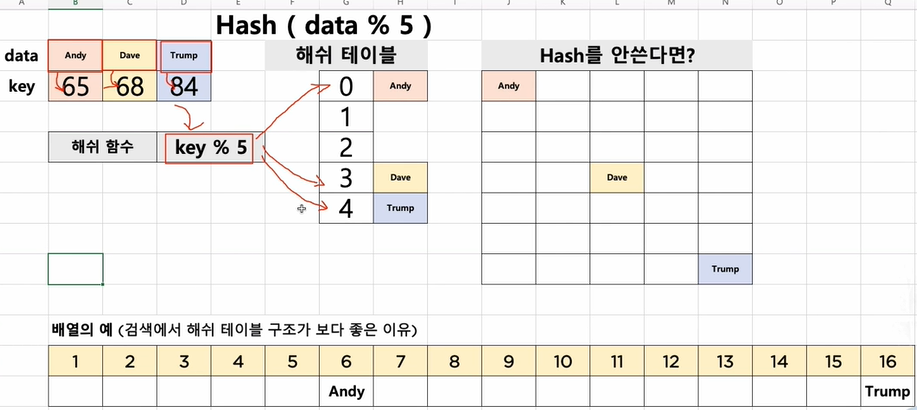
각각 키를 추출할 수 있게끔 하고 해쉬함수를 만들면 해쉬 테이블 특정 슬롯에 저장하는 셈이 된다.
이걸 배열로 만들면?
일일이 하나씩 모든 인덱스 배열을 다 탐색해야 한다. 만약 트럼프면 맨 뒤까지 검색해야.
반면 해쉬함수는 해쉬함수 한번만 돌리면 바로 알아낼 수 있다.
해쉬테이블이라는 구조가 그래서 검색시 굉장히 많이 쓰일 수 있다.
자료 구조 해쉬 테이블의 장단점과 주요 용도
- 장점
- 데이터 저장/읽기 속도가 빠르다. (검색 속도가 빠르다.)
- 해쉬는 키에 대한 데이터가 있는지(중복) 확인이 쉬움
- 단점
- 일반적으로 저장공간이 좀더 많이 필요하다.
- 여러 키에 해당하는 주소가 동일할 경우 충돌을 해결하기 위한 별도 자료구조가 필요함
- 주요 용도
- 검색이 많이 필요한 경우
- 저장, 삭제, 읽기가 빈번한 경우
- 캐쉬 구현시 (중복 확인이 쉽기 때문)
1. 해쉬 함수: key % 8
2. 해쉬 키 생성: hash(data)
hash_table = list([0 for i in range(8)])
def get_key(data):
return hash(data)
def hash_function(key):
return key % 8
def save_data(data, value):
hash_address = hash_function(get_key(data))
hash_table[hash_address] = value
def read_data(data):
hash_address = hash_function(get_key(data))
return hash_table[hash_address]
충돌(Collision) 해결 알고리즘 (좋은 해쉬 함수 사용하기)
- 해쉬 테이블의 가장 큰 문제는 충돌(Collision)의 경우입니다.
- 이 문제를 충돌(Collision) 또는 해쉬 충돌(Hash Collision)이라고 부릅니다.
Chaining 기법
- 개방 해슁 또는 Open Hashing 기법 중 하나: 해쉬 테이블 저장공간 외의 공간을 활용하는 기법
- 충돌이 일어나면, 링크드 리스트라는 자료 구조를 사용해서, 링크드 리스트로 데이터를 추가로 뒤에 연결시켜서 저장하는 기법
해시 충돌 발생하면 그 데이터에 대해서 추가 데이터 공간 확보해서 해결(오픈해싱, 개방해싱이라고 함)
1. 해쉬 함수: key % 8
2. 해쉬 키 생성: hash(data)
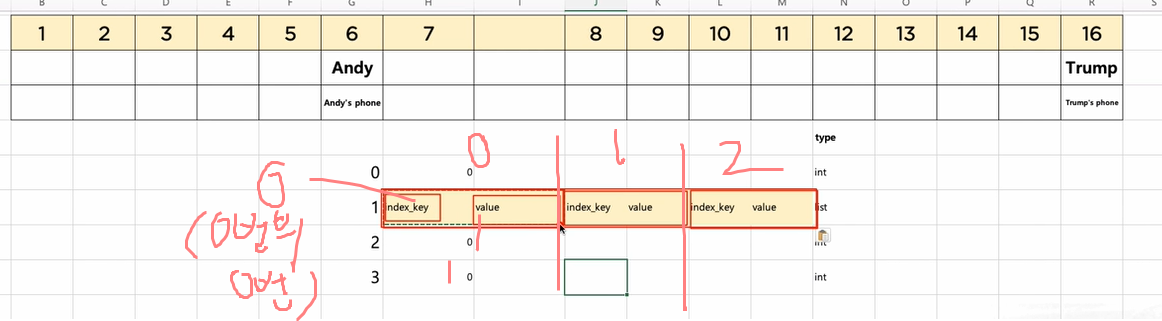
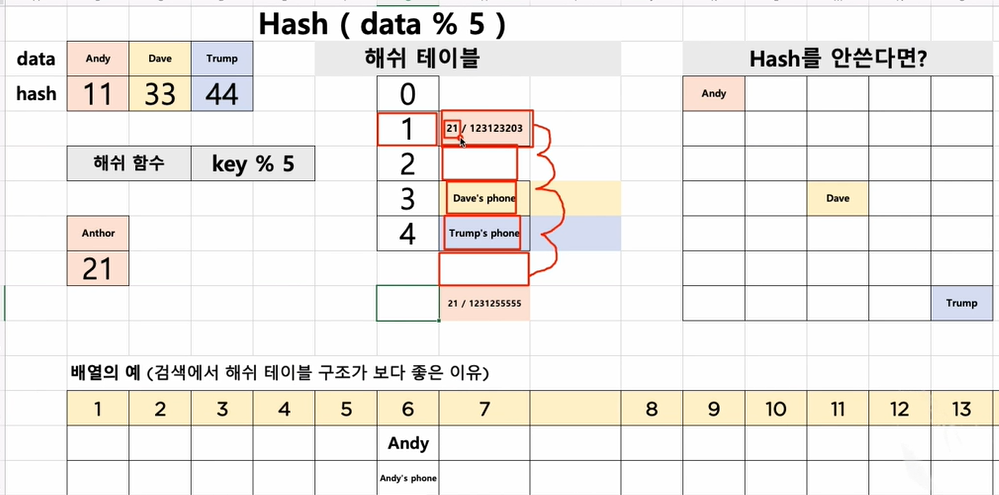
Chaining기법은 충돌 발생시 링크드 리스트로 만들어서 연결시키고 해결한다.
만약 배열로 하면 충돌이 얼마나 일어날 지 모르고 최대 충돌 만큼 배열을 미리 확률 만큼 미리 잡아놔야 하는데, 링크드느 리스트는 충돌이 날떄만 리스트로 데이터 만들면 되서 이렇게 사용이 가능하다.
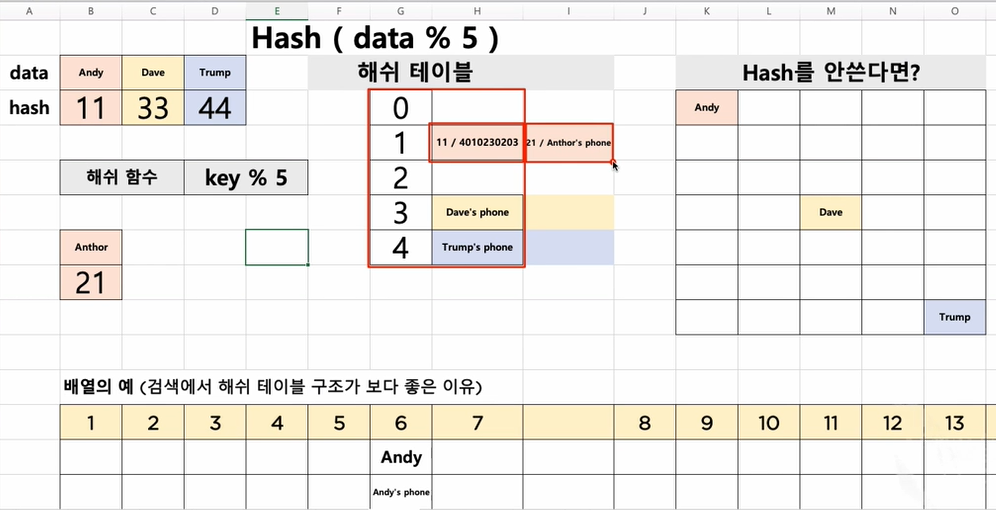
Chaining기법은 빨간색 사각형이 해쉬테이블일 떄 1번처럼 충돌이 일어나면 테이블 밖에 링크드 리스트를 둠.
Linear Probing 기법
- 폐쇄 해슁 또는 Close Hashing 기법 중 하나: 해쉬 테이블 저장공간 안에서 충돌 문제를 해결하는 기법
- 충돌이 일어나면, 해당 hash address의 다음 address부터 맨 처음 나오는 빈공간에 저장하는 기법
- 저장공간 활용도를 높이기 위한 기법
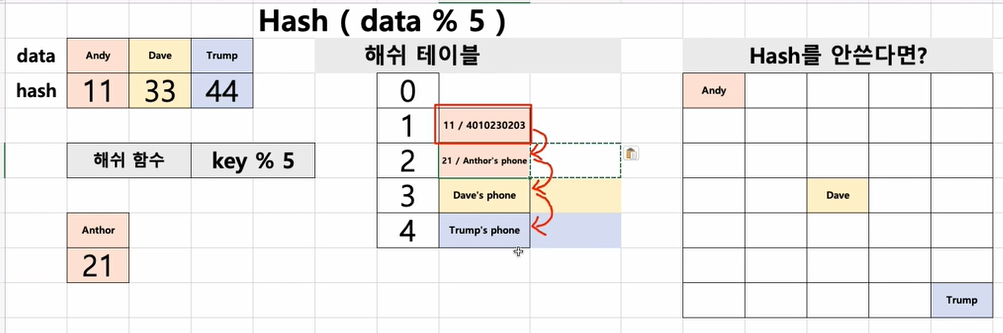
chaining기법과 달리 다음칸 찾으면서 빈 공간이 있으면 그 곳에 데이터를 넣는다.
그 다음칸 확인하면서 빈 공간 최초 확인시 해당 데이터를 넣는게 Linear Probing기법이다.
이 기법의 장점은 저장공간의 활용도를 높일 수 있다는 점이다.
해쉬테이블의 빈 공간을 충돌된 데이터로 채워서 활용도를 높일 수 있다.
def read_data(data):
index_key = get_key(data)
hash_address = hash_function(index_key)
if hash_table[hash_address] != 0: #0인지를 봐야한다.
for index in range(hash_address, len(hash_table)):
if hash_table[index] == 0:
return None#없다는 표시로 none 리턴
elif hash_table[index][0] == index_key: #만약 인덱스 키라면
#내가 원하는 키라면 ? 해당 데이터 값을 리턴해준다. 그럼 이 for문은 끝남
#근데 만약 이 조건이 부합하는건 어느 순간 데이터가 다 안맞는데 한번도 저장이 된적이 없으면?
#해당 데이터에 대한 값이 한번도 저장된 적이 없다.
#그것이 빈 공간이 있다는 것에 걸려서 None을 리턴한다.
return hash_table[index][1]
else:
return None
Linear Probing기법은 테이블에 해당 데이터 주소가 저장되어 있을 때 키값을 가지고 판단하고 충돌이 일어나 면 동일한 데이터 주소라도 다음 빈공간 찾아서 저장을 한다.
찾을 때도 데이터가 있다고 바로 그냥 꺼내는 게 아니라 키값을 확인하고 키값이 맞을때 까지 데이터를 빈슬롯을 순회한다.
키값이 맞는 걸 매칭하면 해당 데이터를 리턴한다.
빈번한 충돌을 개선하는 기법
- 해쉬 함수을 재정의 및 해쉬 테이블 저장공간을 확대
- 예:
hash_table = list([None for i in range(16)])
def hash_function(key):
return key % 16
해쉬 함수와 키 생성 함수
- 파이썬의 hash() 함수는 실행할 때마다, 값이 달라질 수 있음
- 유명한 해쉬 함수들이 있음: SHA(Secure Hash Algorithm, 안전한 해시 알고리즘)
- 어떤 데이터도 유일한 고정된 크기의 고정값을 리턴해주므로, 해쉬 함수로 유용하게 활용 가능
시간 복잡도
- 일반적인 경우(Collision이 없는 경우)는 O(1)(충돌이 없는 경우 입력값이 1개든 10개든 100만개든 맞는 해쉬 공간에 진행하면 됨.만약 충돌이 없다면 O(n)이 걸린다.)
- 최악의 경우(Collision이 모두 발생하는 경우)는 O(n) (이 경우는 모든 경우에 충돌이 일어나는 경우다.)
해쉬 테이블의 경우, 일반적인 경우를 기대하고 만들기 때문에, 시간 복잡도는 O(1) 이라고 말할 수 있음
검색에서 해쉬 테이블의 사용 예
- 16개의 배열에 데이터를 저장하고, 검색할 때 O(n) (이 경우는 모든 경우 순회)
- 16개의 데이터 저장공간을 가진 위의 해쉬 테이블에 데이터를 저장하고, 검색할 때 O(1) (공간 슬롯 많이 만들어 놓고 해쉬함수를 특정ㅎ저장공간에 저장하거나 불러오는 경우)
저장과 검색에 있어서 아주 효율적인 자료구조이다.
트리(Tree)
- 면접관이나 시니어 개발자들도 자료구조 알고리즘 잘 모르는 경우도 많지만 트리는 복잡한 자료구조에서도 꼭 묻거나 자주 면접때 물어보므로 이건 꼭 알아두자. 시니어 개발자들도 트리는 꼭 중요하게 생각하는 경우가 많다.
트리 (Tree) 구조
- 트리: Node와 Branch를 이용해서, 사이클을 이루지 않도록 구성한 데이터 구조
- 실제로 어디에 많이 사용되나?
- 트리 중 이진 트리 (Binary Tree) 형태의 구조로, 탐색(검색) 알고리즘 구현을 위해 많이 사용됨
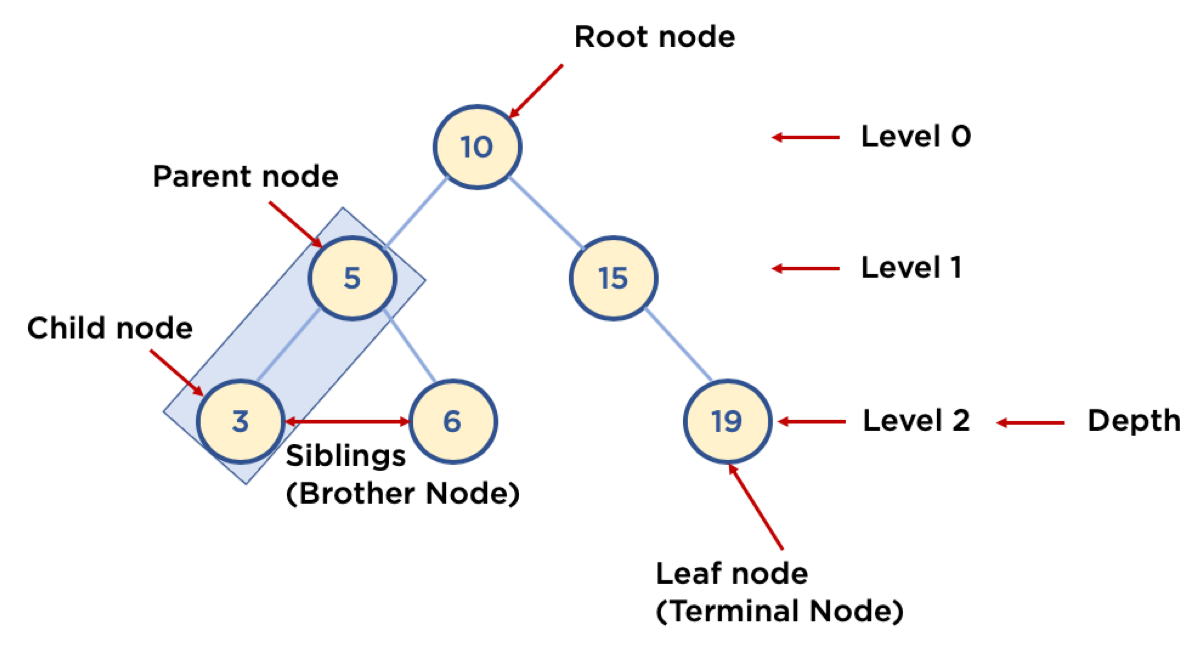
관련 용어
- Node: 트리에서 데이터를 저장하는 기본 요소 (데이터와 다른 연결된 노드에 대한 Branch 정보 포함)
- Root Node: 트리 맨 위에 있는 노드
- Level: 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
- Parent Node: 어떤 노드의 다음 레벨에 연결된 노드
- Child Node: 어떤 노드의 상위 레벨에 연결된 노드
- Leaf Node (Terminal Node): Child Node가 하나도 없는 노드
- Sibling (Brother Node): 동일한 Parent Node를 가진 노드
- Depth: 트리에서 Node가 가질 수 있는 최대 Level
이진 트리와 이진 탐색 트리 (Binary Search Tree)
- 이진 트리: 노드의 최대 Branch가 2인 트리
- 이진 탐색 트리 (Binary Search Tree, BST): 이진 트리에 다음과 같은 추가적인 조건이 있는 트리
- 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가지고 있음!

(출처: https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node)
자료 구조 이진 탐색 트리의 장점과 주요 용도
- 주요 용도: 데이터 검색(탐색)
- 장점: 탐색 속도를 개선할 수 있음
단점은 이진 탐색 트리 알고리즘 이해 후에 살펴보기로 함
바이너리 서치 트리가 혁신적으로 탐색 시간을 줄여줄 수 있다.
이진트리와 정렬된 배열간의 탐색 비교
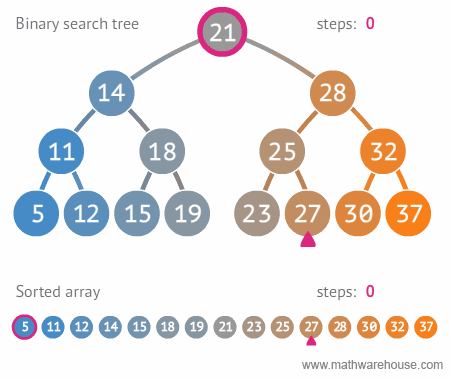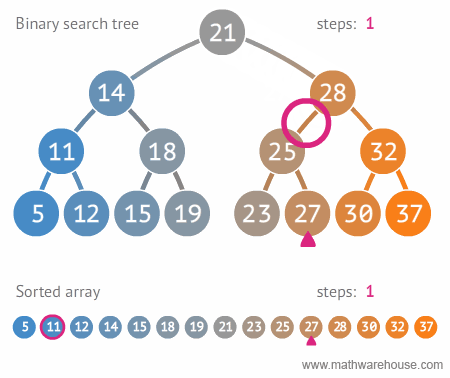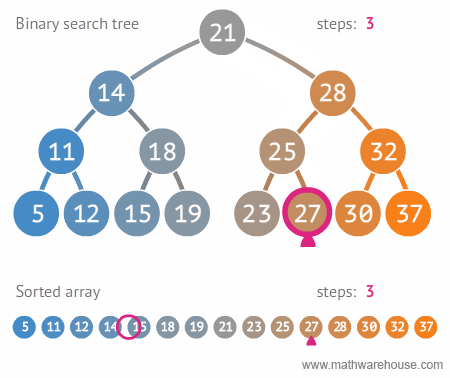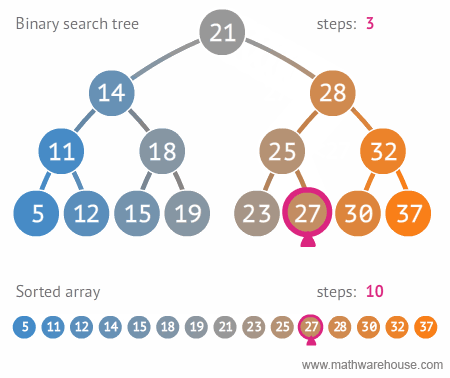
(출처: https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node)
트리는 브랜치와 노드로 구성된 사이클 가진 자료구조
이진트리는 거기에 덧붙여서 브랜치 노드가 가질수 있는 최대 노드의 개수가 2개, 이진 탐색트리는 하나 더 붙여서 브랜치 만들떄 작은건 왼쪽, 큰건 오른쪽.
실제로 데이터 탐색시 이진탐색트리에 따라 작다 크다에 따라 탐색해서 빠른 탐색이 가능하다.
이진 탐색 트리 삭제
- 매우 복잡함. 경우를 나누어서 이해하는 것이 좋음
Leaf Node 삭제
- Leaf Node: Child Node 가 없는 Node
- 삭제할 Node의 Parent Node가 삭제할 Node를 가리키지 않도록 한다.
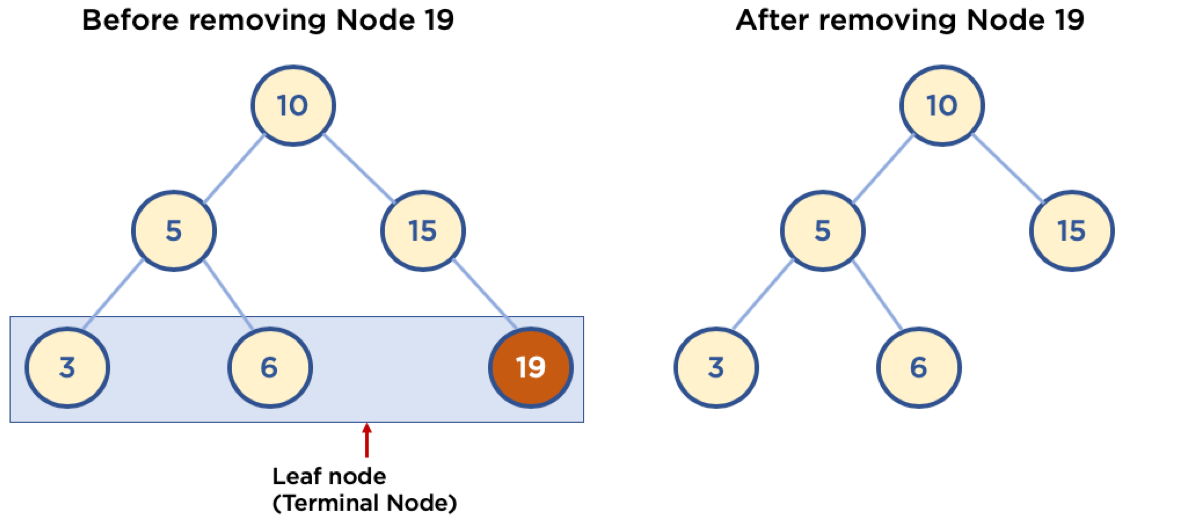
Child Node 가 하나인 Node 삭제
- 삭제할 Node의 Parent Node가 삭제할 Node의 Child Node를 가리키도록 한다.
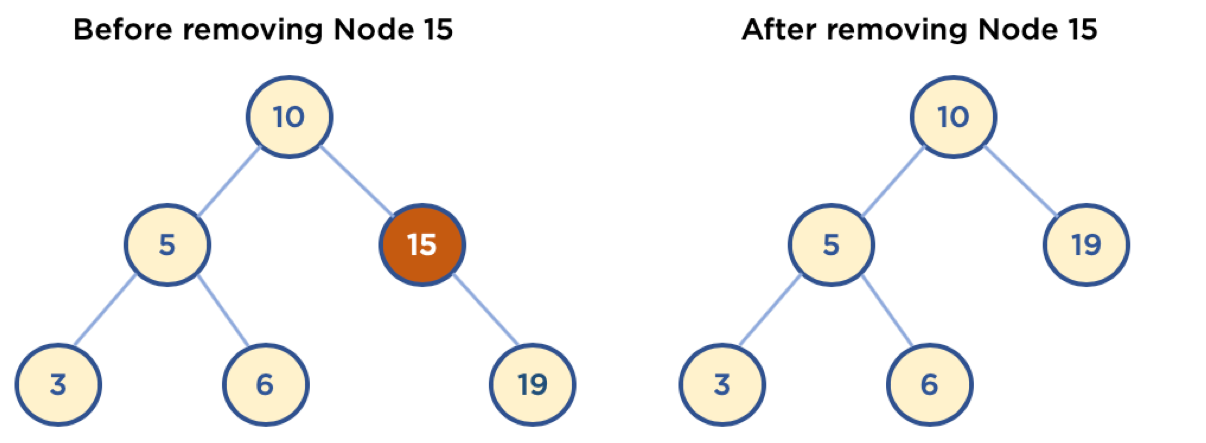
Child Node 가 두 개인 Node 삭제
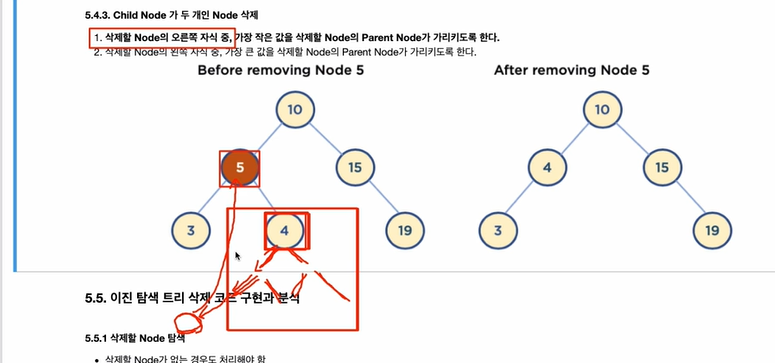
- 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키도록 한다.
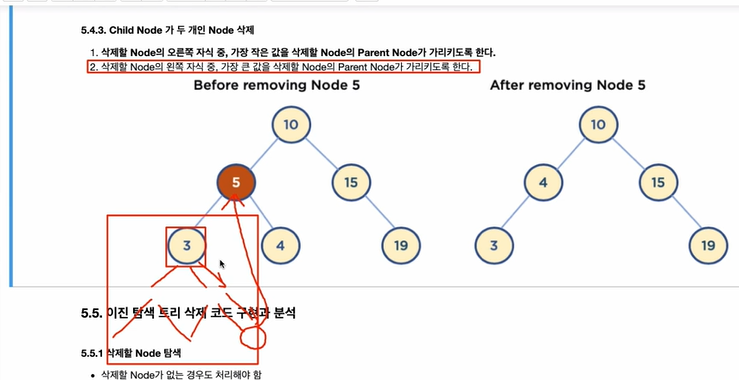
- 삭제할 Node의 왼쪽 자식 중, 가장 큰 값을 삭제할 Node의 Parent Node가 가리키도록 한다.
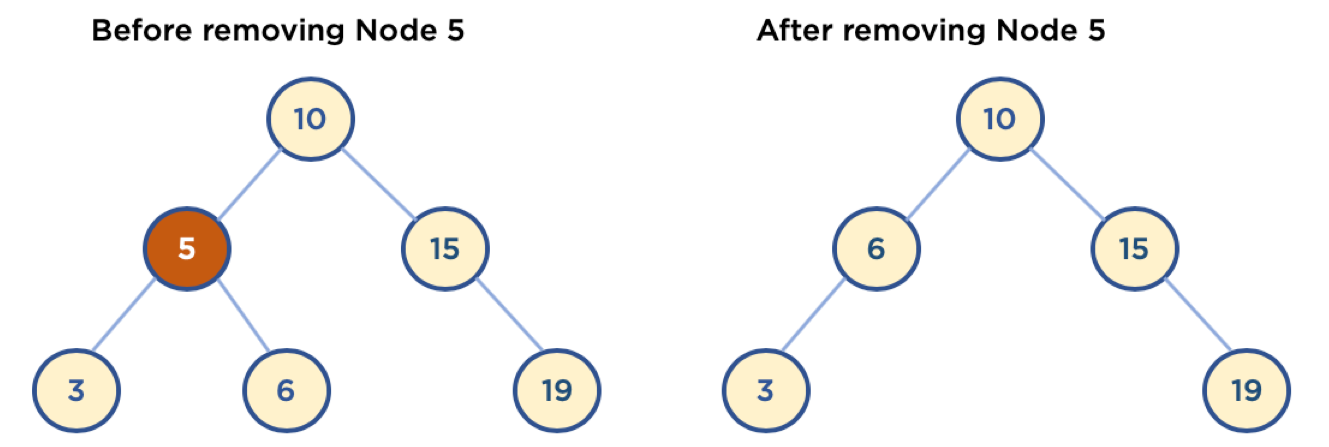
그렇게 되면 우측 그림들 처럼 트리의 형태가 깨지지 않게 된다.
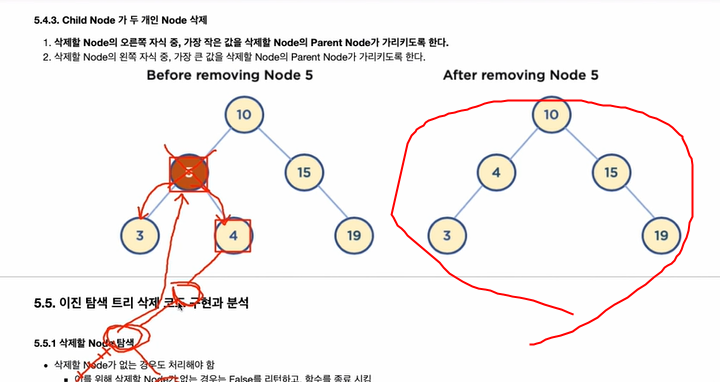
삭제할 Node의 오른쪽 자식중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키게 할 경우
(이런식으로 복잡한 문제 만났을 때 divide and conquer로 해결해나가면 된다.)
- 삭제할 Node의 오른쪽 자식 선택
- 오른쪽 자식의 가장 왼쪽에 있는 Node를 선택
- 해당 Node를 삭제할 Node의 Parent Node의 왼쪽 Branch가 가리키게 함
- 해당 Node의 왼쪽 Branch가 삭제할 Node의 왼쪽 Child Node를 가리키게 함
- 해당 Node의 오른쪽 Branch가 삭제할 Node의 오른쪽 Child Node를 가리키게 함
- 만약 해당 Node가 오른쪽 Child Node를 가지고 있었을 경우에는, 해당 Node의 본래 Parent Node의 왼쪽 Branch가 해당 오른쪽 Child Node를 가리키게 함
프로그래밍에서 가장 많이 쓰는 알고리즘이 devide and conquer이다.복잡한 문제 만나도 각각의 문제를 잘게 쪼개서 해결하자. 코드로 구현하긴 어렵긴 하지만 면접에서 이런걸 설명하거나 실제로 만들거나 하기엔 어렵고 불가능하긴하다.
이진 탐색 트리 삭제 코드 구현과 분석
삭제할 Node 탐색
- 삭제할 Node가 없는 경우도 처리해야 함
- 이를 위해 삭제할 Node가 없는 경우는 False를 리턴하고, 함수를 종료 시킴
# def delete(self, value):
searched = False
self.current_node = self.head
self.parent = self.head
while self.current_node:
if self.current_node.value == value: #current 노드가 value인지 보고 value면 바로 끝남(찾았으니까)
searched = True#true로 바꾸고 반복문 탈출
break
elif value < self.current_node.value:#만약 노드에서 삭제할 노드가 아니라면 찾아야
self.parent = self.current_node
self.current_node = self.current_node.left
else: #그렇지 않다면 같거나 크다
self.parent = self.current_node
self.current_node = self.current_node.right
if searched == False:#이 구문을 뛰어 넘어서 이 구문 실행할 상황이 오면
return False
### 이후부터 Case들을 분리해서, 코드 작성
Case1: 삭제할 Node가 Leaf Node인 경우
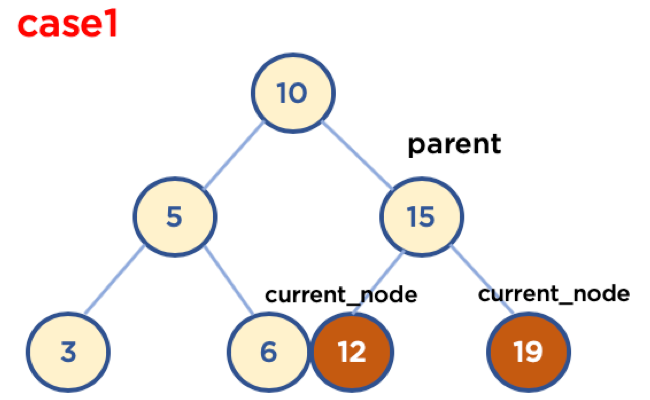
# self.current_node 가 삭제할 Node, self.parent는 삭제할 Node의 Parent Node인 상태
if self.current_node.left == None and self.current_node.right == None:
if value < self.parent.value:
self.parent.left = None#Parent의 입장에서 보는거(작다면 self.parent의 좌측이 none이 되어야)
else:
self.parent.right = None
del self.current_node#
Case2: 삭제할 Node가 Child Node를 한 개 가지고 있을 경우
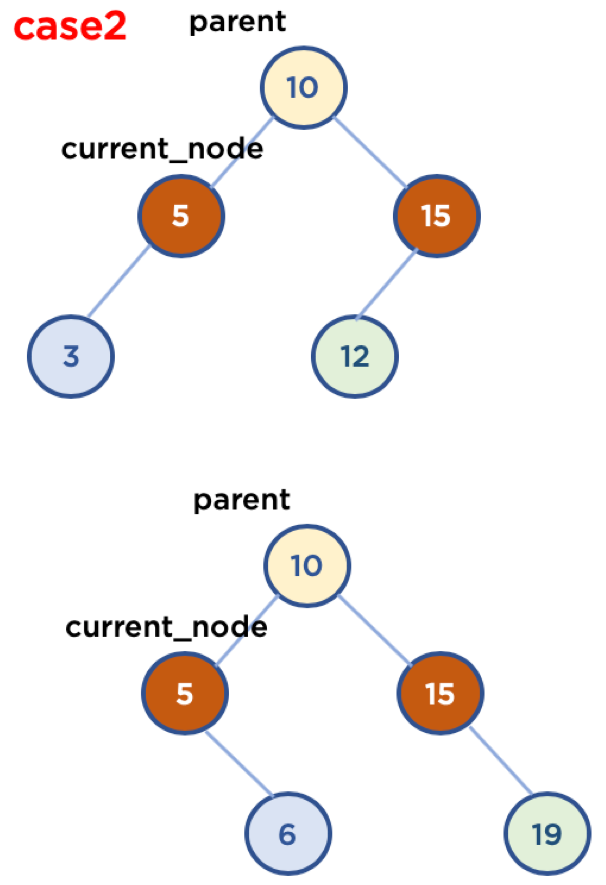
if self.current_node.left != None and self.current_node.right == None:
if value < self.parent.value:#왼쪽에 존재하는거 지우고 그럼 그 노드 아래(자식노드)주소 가리키게 해야 그럼 그 자식노드가 루트노드 바라보게 해야한다
self.parent.left = self.current_node.left
else:#이건 반대로 오른쪽일때(삭제되는 노드가)
self.parent.right = self.current_node.left
elif self.current_node.left == None and self.current_node.right != None:
#이 경우는 오른쪽에만 노드가 존재하는 경우다.
if value < self.parent.value:
self.parent.left = self.current_node.right
else:
self.parent.right = self.current_node.right
self.current_node 가 삭제할 Node, self.parent는 삭제할 Node의 Parent Node인 상태
if self.current_node.left == None and self.current_node.right == None:
if value < self.parent.value:
self.parent.left = None#Parent의 입장에서 보는거(작다면 self.parent의 좌측이 none이 되어야)
else:
self.parent.right = None
del self.current_node#
Case3-1: 삭제할 Node가 Child Node를 두 개 가지고 있을 경우 (삭제할 Node가 Parent Node 왼쪽에 있을 때)
삭제할 노드가 부모노드 왼쪽, 오른쪽 있을떄 삭제 할 때 방법이 또 갈린다.
- 기본 사용 가능 전략
- 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키도록 한다.
- 삭제할 Node의 왼쪽 자식 중, 가장 큰 값을 삭제할 Node의 Parent Node가 가리키도록 한다.
- 기본 사용 가능 전략 중, 1번 전략을 사용하여 코드를 구현하기로 함
- 경우의 수가 또다시 두가지가 있음
- Case3-1-1: 삭제할 Node가 Parent Node의 왼쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 Child Node가 없을 때
- Case3-1-2: 삭제할 Node가 Parent Node의 왼쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 오른쪽에 Child Node가 있을 때
- 가장 작은 값을 가진 Node의 Child Node가 왼쪽에 있을 경우는 없음, 왜냐하면 왼쪽 Node가 있다는 것은 해당 Node보다 더 작은 값을 가진 Node가 있다는 뜻이기 때문임
- 경우의 수가 또다시 두가지가 있음
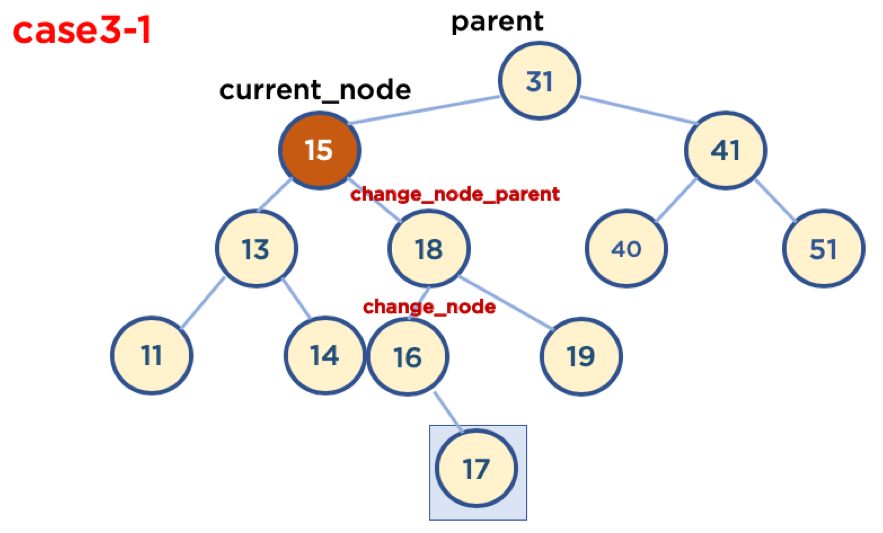
if self.current_node.left != None and self.current_node.right != None: # case3
if value < self.parent.value: # case3-1
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
while self.change_node.left != None:
self.change_node_parent = self.change_node
self.change_node = self.change_node.left
if self.change_node.right != None:
self.change_node_parent.left = self.change_node.right
else:
self.change_node_parent.left = None
self.parent.left = self.change_node
self.change_node.right = self.current_node.right
self.change_node.left = self.change_node.left
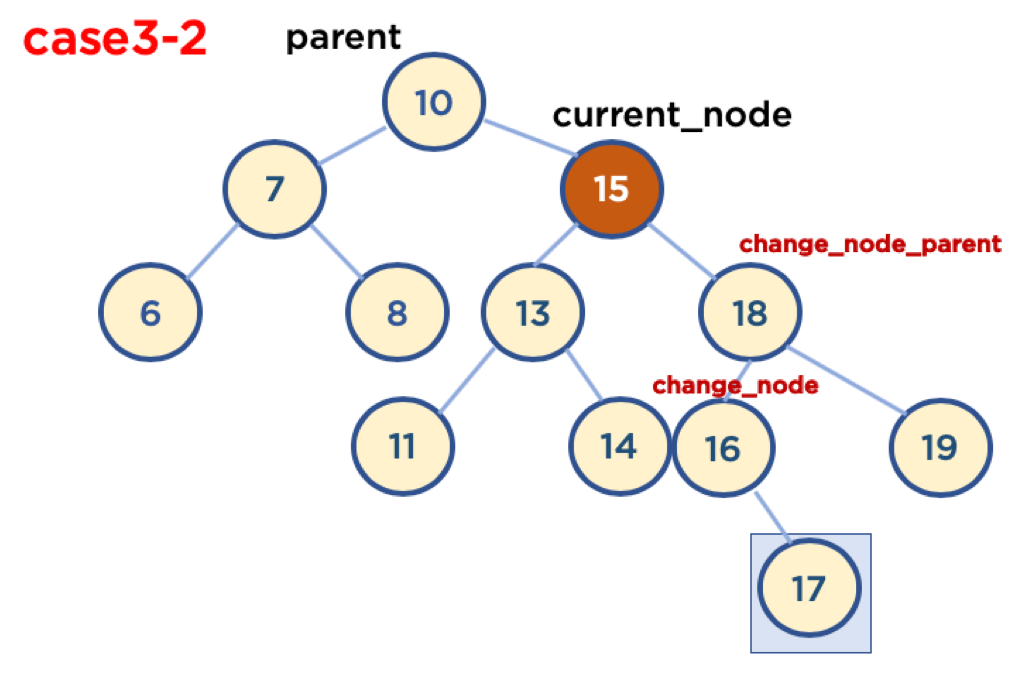
Case3-2: 삭제할 Node가 Child Node를 두 개 가지고 있을 경우 (삭제할 Node가 Parent Node 오른쪽에 있을 때)
- 기본 사용 가능 전략
- 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키도록 한다.
- 삭제할 Node의 왼쪽 자식 중, 가장 큰 값을 삭제할 Node의 Parent Node가 가리키도록 한다.
- 기본 사용 가능 전략 중, 1번 전략을 사용하여 코드를 구현하기로 함
- 경우의 수가 또다시 두가지가 있음
- Case3-2-1: 삭제할 Node가 Parent Node의 오른쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 Child Node가 없을 때
- Case3-2-2: 삭제할 Node가 Parent Node의 오른쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 오른쪽에 Child Node가 있을 때
- 가장 작은 값을 가진 Node의 Child Node가 왼쪽에 있을 경우는 없음, 왜냐하면 왼쪽 Node가 있다는 것은 해당 Node보다 더 작은 값을 가진 Node가 있다는 뜻이기 때문임
- 경우의 수가 또다시 두가지가 있음
else:
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
while self.change_node.left != None:
self.change_node_parent = self.change_node
self.change_node = self.change_node.left
if self.change_node.right != None:
self.change_node_parent.left = self.change_node.right
else:
self.change_node_parent.left = None
self.parent.right = self.change_node
self.change_node.left = self.current_node.left
self.change_node.right = self.current_node.right
전체 코드
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class NodeMgmt: #여기서 이진탐색 트리가 되는 것
def __init__(self, head):
self.head = head
def insert(self, value):
self.current_node = self.head
while True:
if value < self.current_node.value:
if self.current_node.left != None:
self.current_node = self.current_node.left
else:
self.current_node.left = Node(value)
break
else:
if self.current_node.right != None:
self.current_node = self.current_node.right
else:
self.current_node.right = Node(value)
break
def search(self, value):
self.current_node = self.head
while self.current_node:
if self.current_node.value == value:
return True
elif value < self.current_node.value:
self.current_node = self.current_node.left
else:
self.current_node = self.current_node.right
return False
def delete(self, value):
# 삭제할 노드 탐색
searched = False
self.current_node = self.head
self.parent = self.head
while self.current_node:
if self.current_node.value == value:
searched = True
break
elif value < self.current_node.value:
self.parent = self.current_node
self.current_node = self.current_node.left
else:
self.parent = self.current_node
self.current_node = self.current_node.right
if searched == False:
return False
# case1
if self.current_node.left == None and self.current_node.right == None:
if value < self.parent.value:
self.parent.left = None
else:
self.parent.right = None
# case2
elif self.current_node.left != None and self.current_node.right == None:
if value < self.parent.value:
self.parent.left = self.current_node.left
else:
self.parent.right = self.current_node.left
elif self.current_node.left == None and self.current_node.right != None:
if value < self.parent.value:
self.parent.left = self.current_node.right
else:
self.parent.right = self.current_node.right
# case 3
elif self.current_node.left != None and self.current_node.right != None:
# case3-1
if value < self.parent.value:
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
while self.change_node.left != None:
self.change_node_parent = self.change_node
self.change_node = self.change_node.left
if self.change_node.right != None:
self.change_node_parent.left = self.change_node.right
else:
self.change_node_parent.left = None
self.parent.left = self.change_node
self.change_node.right = self.current_node.right
self.change_node.left = self.change_node.left
# case 3-2
else:
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
while self.change_node.left != None:
self.change_node_parent = self.change_node
self.change_node = self.change_node.left
if self.change_node.right != None:
self.change_node_parent.left = self.change_node.right
else:
self.change_node_parent.left = None
self.parent.right = self.change_node
self.change_node.right = self.current_node.right
self.change_node.left = self.current_node.left
return True
사실 각 케이스마다 테스트 케이스 만들어서 하는것이 가장 좋긴 하다.
이진 탐색 트리의 시간 복잡도와 단점
시간 복잡도 (탐색시)
- 이진탐색트리는 depth와 관련있다.
- depth (트리의 높이) 를 h라고 표기한다면, O(h)
- n개의 노드를 가진다면, $h = log_2{n} $ 에 가까우므로, 시간 복잡도는 $ O(log{n}) $
- 참고: 빅오 표기법에서 $log{n}$ 에서의 log의 밑은 10이 아니라, 2입니다.
- 한번 실행시마다, 50%의 실행할 수도 있는 명령을 제거한다는 의미. 즉 50%의 실행시간을 단축시킬 수 있다는 것을 의미함

- 한번 실행시마다, 50%의 실행할 수도 있는 명령을 제거한다는 의미. 즉 50%의 실행시간을 단축시킬 수 있다는 것을 의미함
- 참고: 빅오 표기법에서 $log{n}$ 에서의 log의 밑은 10이 아니라, 2입니다.
(출처: https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node)
이진 탐색 트리 단점
- 평균 시간 복잡도는 $ O(log{n}) $ 이지만,
- 이는 트리가 균형잡혀 있을 때의 평균 시간복잡도이며,
- 다음 예와 같이 구성되어 있을 경우, 최악의 경우는 링크드 리스트등과 동일한 성능을 보여줌 ( $O(n)$ )
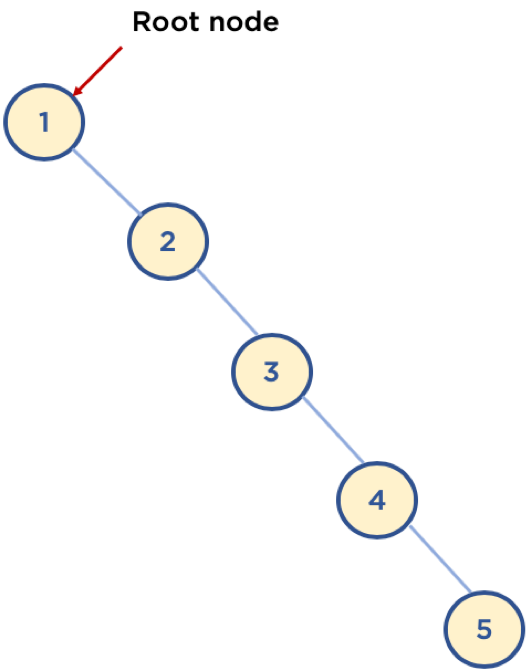
최악의 경우로 만약 다음과 같은 이진트리에서 5라는 데이터를 찾기위해 탐색하면 마지막 까지 탐색해야 된다.(O(n)의 시간복잡도를 지니게 된다.)
힙(heap)
힙 (Heap) 이란?
- 힙: 데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)
- 완전 이진 트리: 노드를 삽입할 때 최하단 왼쪽 노드부터 차례대로 삽입하는 트리
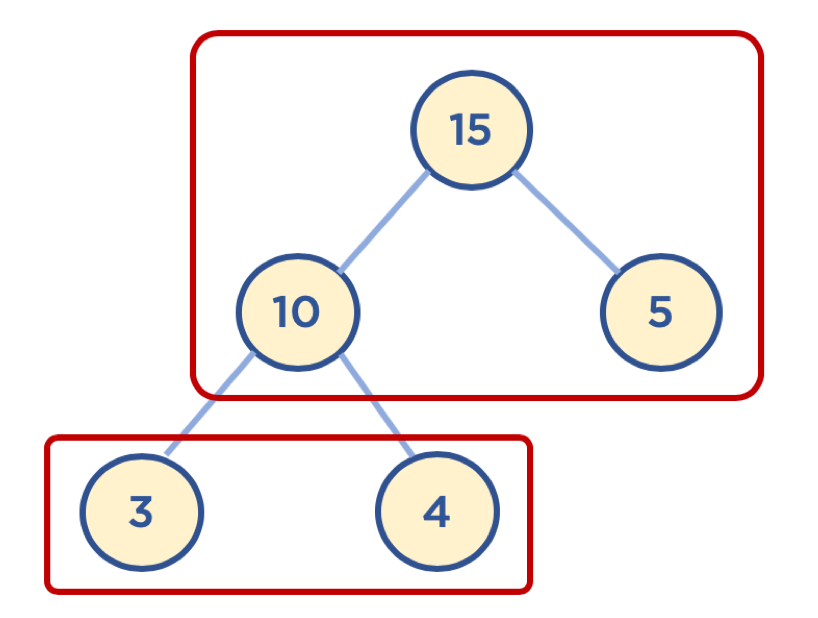
- 힙을 사용하는 이유
- 배열에 데이터를 넣고, 최대값과 최소값을 찾으려면 O(n) 이 걸림
- 이에 반해, 힙에 데이터를 넣고, 최대값과 최소값을 찾으면, $ O(log n) $ 이 걸림
- 우선순위 큐와 같이 최대값 또는 최소값을 빠르게 찾아야 하는 자료구조 및 알고리즘 구현 등에 활용됨
힙 (Heap) 구조
- 힙은 최대값을 구하기 위한 구조 (최대 힙, Max Heap) 와, 최소값을 구하기 위한 구조 (최소 힙, Min Heap) 로 분류할 수 있음
- 힙은 다음과 같이 두 가지 조건을 가지고 있는 자료구조임
- 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 같다. (최대 힙의 경우)
- 최소 힙의 경우는 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 작음
- 완전 이진 트리 형태를 가짐
- 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 같다. (최대 힙의 경우)
힙과 이진 탐색 트리의 공통점과 차이점
- 공통점: 힙과 이진 탐색 트리는 모두 이진 트리임
- 차이점:
- 힙은 각 노드의 값이 자식 노드보다 크거나 같음(Max Heap의 경우)
- 이진 탐색 트리는 왼쪽 자식 노드의 값이 가장 작고, 그 다음 부모 노드, 그 다음 오른쪽 자식 노드 값이 가장 큼
- 힙은 이진 탐색 트리의 조건인 자식 노드에서 작은 값은 왼쪽, 큰 값은 오른쪽이라는 조건은 없음
- 힙의 왼쪽 및 오른쪽 자식 노드의 값은 오른쪽이 클 수도 있고, 왼쪽이 클 수도 있음
- 이진 탐색 트리는 탐색을 위한 구조, 힙은 최대/최소값 검색을 위한 구조 중 하나로 이해하면 됨
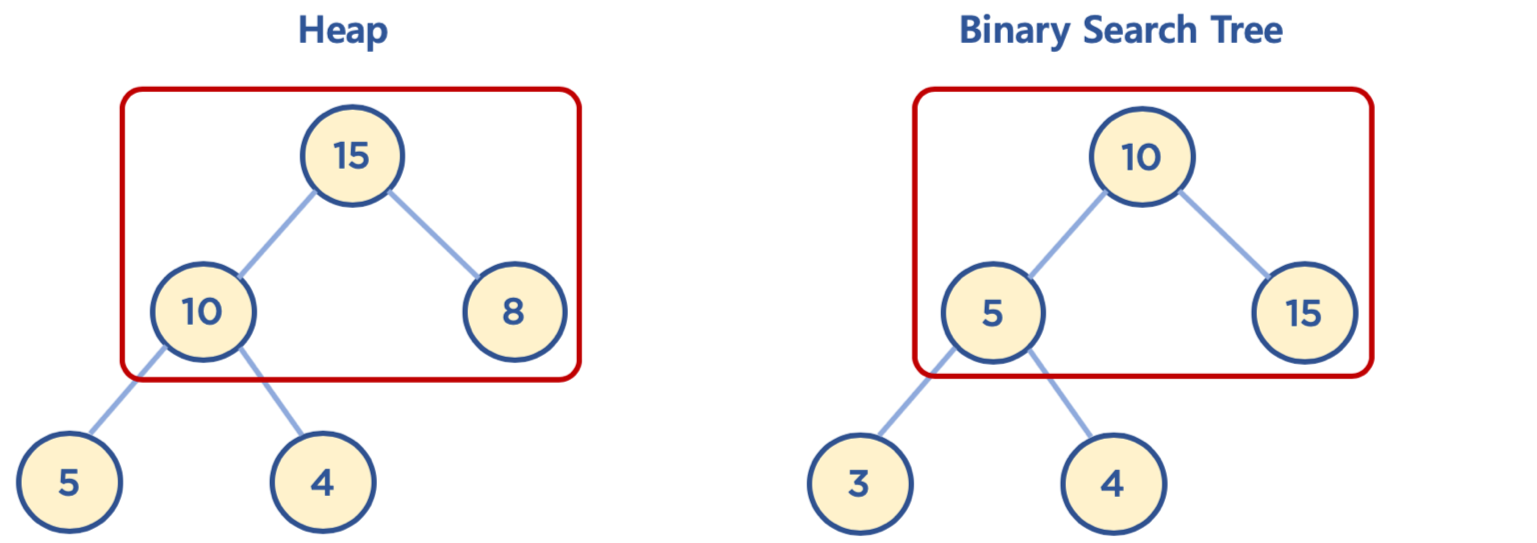
힙 (Heap) 동작
- 데이터를 힙 구조에 삽입, 삭제하는 과정을 그림을 통해 선명하게 이해하기
힙에 데이터 삽입하기 - 기본 동작
- 힙은 완전 이진 트리이므로, 삽입할 노드는 기본적으로 왼쪽 최하단부 노드부터 채워지는 형태로 삽입
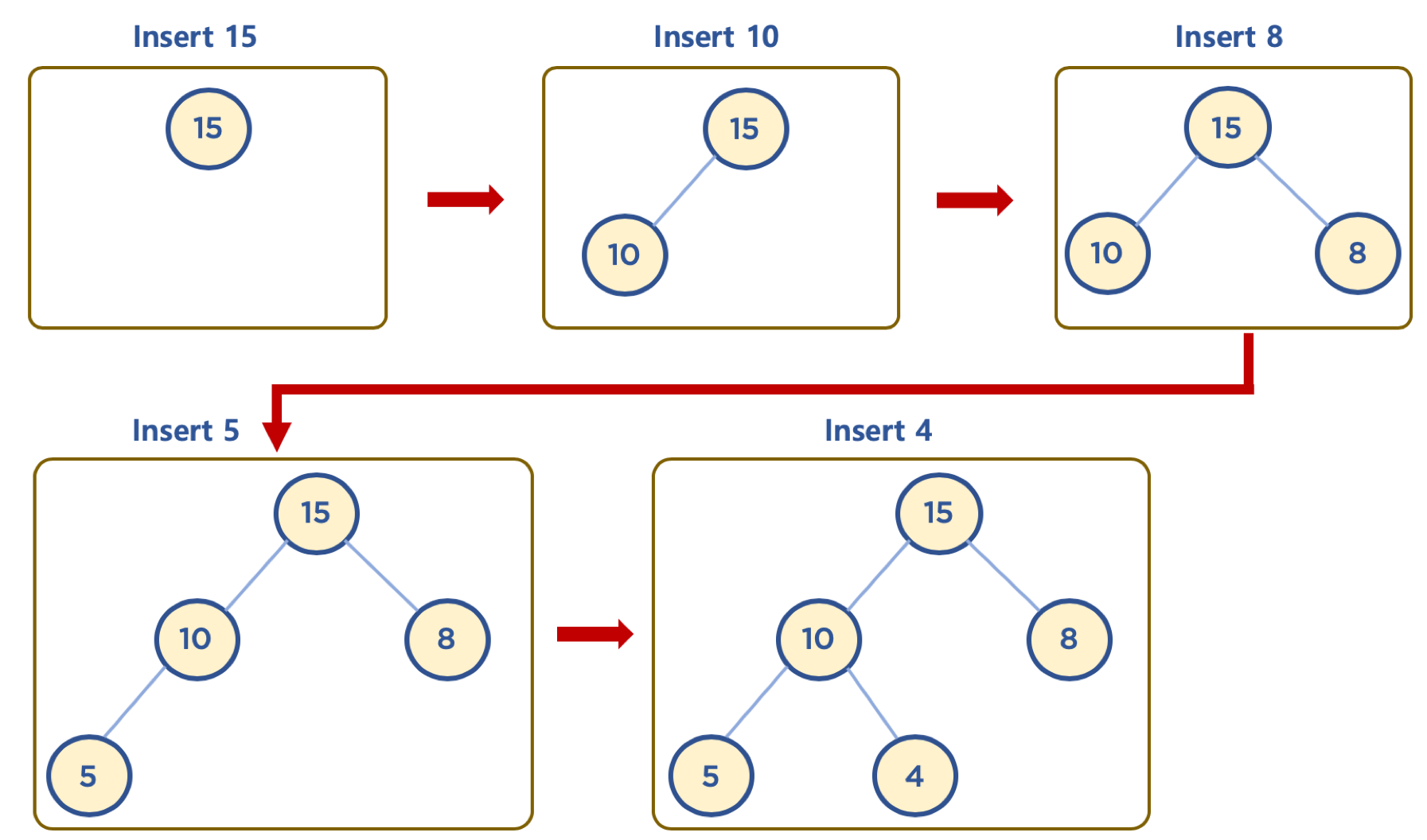
힙에 데이터 삽입하기 - 삽입할 데이터가 힙의 데이터보다 클 경우 (Max Heap 의 예)
- 먼저 삽입된 데이터는 완전 이진 트리 구조에 맞추어, 최하단부 왼쪽 노드부터 채워짐
- 채워진 노드 위치에서, 부모 노드보다 값이 클 경우, 부모 노드와 위치를 바꿔주는 작업을 반복함 (swap)
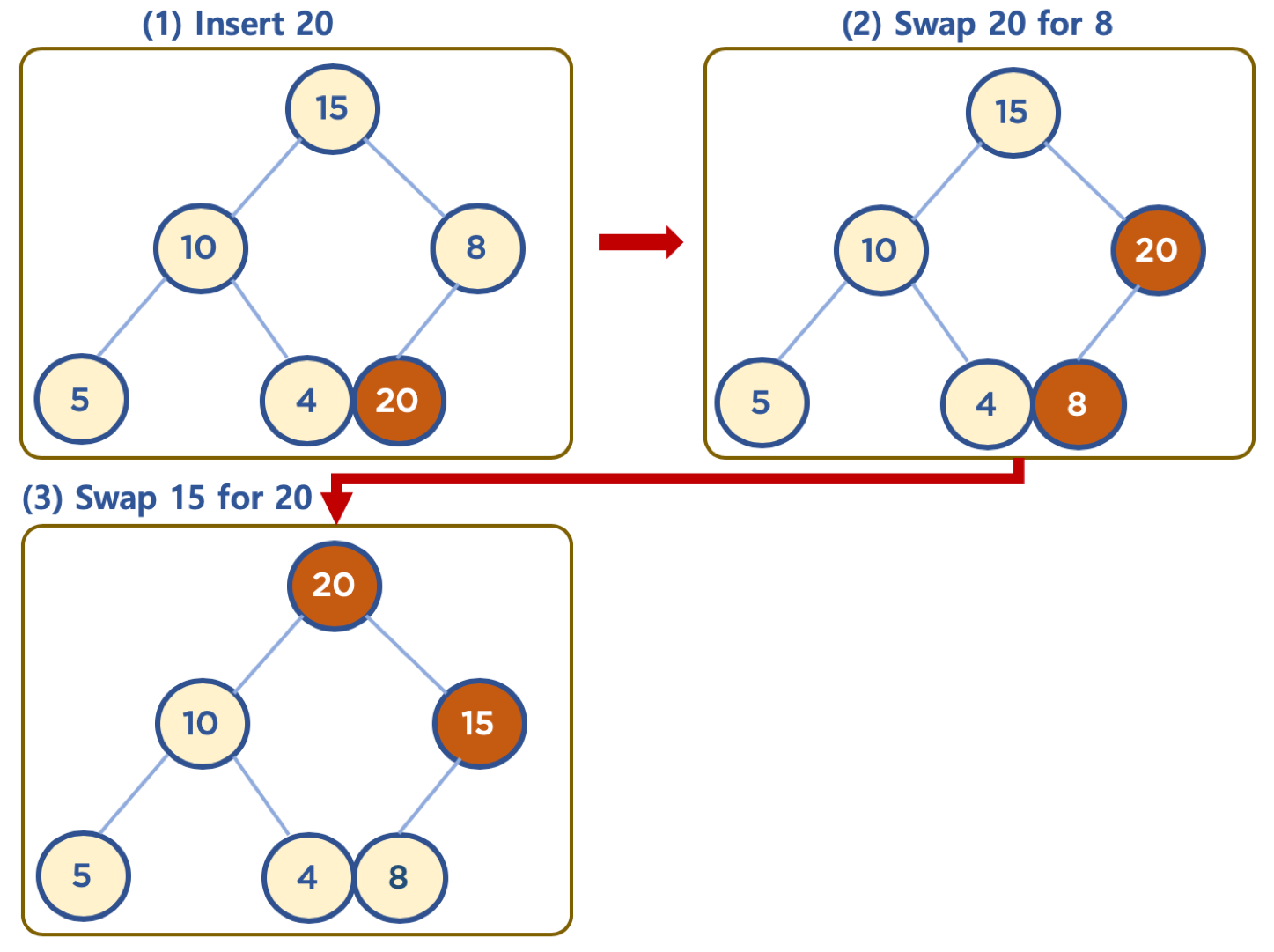
부모노드랑 자식노드랑 비교했는데 부모노드가 자식노드보다 크면 더 바꾸맆ㄹ요 없다.
ㅇㅇ
데이터 삽입은 2가지 단계가 있다.
- 완전 이진트리에 맞춰서 왼쪽 자식노드부터 채워가는거.
- 채운 후에는 그 노드의 부모노드와 비교해서 이 자식노드가 부모노드보다 작을 때 까지 바꿔주는 작업을 반복해줌. 그래야 데이터 삽입이 가능하다.
힙의 데이터 삭제하기 (Max Heap 의 예)
여기서 Max Heap은 최대값이 루트노드에 이미 있다. 맨 처음에 하는 일은 루트노드에 있는 값을 끌어낸다. 삭제하면 보통 맨 위에 있는걸 먼저 삭제함(그 아래 자식노드들을 먼저 지우진 않음)
루트노드를 삭제하면 트리구조가 유지 될수 없다. 그래서 루트노드를 삭제하면 가장 마지막에 들어갔던 데이터를 (노드를) 맨 위로 올린다.
이 노드를 맨 위로 올리고 힙의 조건중인 하나인 자식노드보다 부모노드가 커야한다는게 일반적으로 깨질수 있으므로 맨 마지막 넣은 값을 루트노드로 올리고 자식노드중 큰 값을(왼쪽이 클지 오른쪽이 클지 모른다.) 비교해서 큰 값을 부모노드와 바꾼다. 그리고 바꾼 뒤에도 부모였던 노드가 자식노드쪽으로 바뀌면 거기서도 비교를해서 그 자식노드와 현 노드를 바꿀 수 있는지 확인하고 가능하다면 또 다시 교환이 일어난다.
그렇게 완전 이진트리 형태를 가지게 만든다.
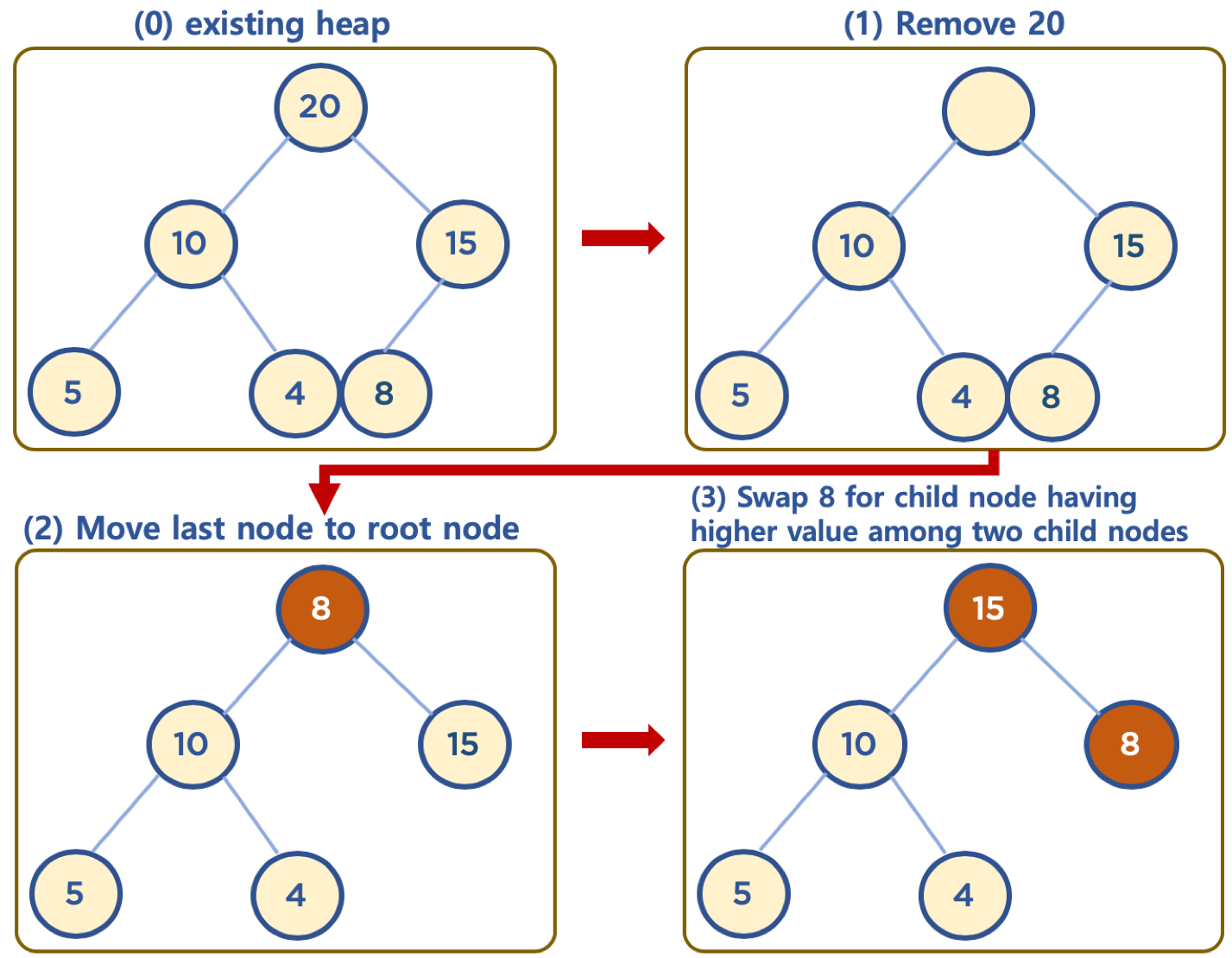
- 보통 삭제는 최상단 노드 (root 노드)를 삭제하는 것이 일반적임
- 힙의 용도는 최대값 또는 최소값을 root 노드에 놓아서, 최대값과 최소값을 바로 꺼내 쓸 수 있도록 하는 것임
- 상단의 데이터 삭제시, 가장 최하단부 왼쪽에 위치한 노드 (일반적으로 가장 마지막에 추가한 노드) 를 root 노드로 이동
- root 노드의 값이 child node 보다 작을 경우, root 노드의 child node 중 가장 큰 값을 가진 노드와 root 노드 위치를 바꿔주는 작업을 반복함 (swap)
힙 구현
힙과 배열
- 일반적으로 힙 구현시 배열 자료구조를 활용함
- 배열은 인덱스가 0번부터 시작하지만, 힙 구현의 편의를 위해, root 노드 인덱스 번호를 1로 지정하면, 구현이 좀더 수월함
- 부모 노드 인덱스 번호 (parent node’s index) = 자식 노드 인덱스 번호 (child node’s index) // 2
- 왼쪽 자식 노드 인덱스 번호 (left child node’s index) = 부모 노드 인덱스 번호 (parent node’s index) * 2
- 오른쪽 자식 노드 인덱스 번호 (right child node’s index) = 부모 노드 인덱스 번호 (parent node’s index) * 2 + 1
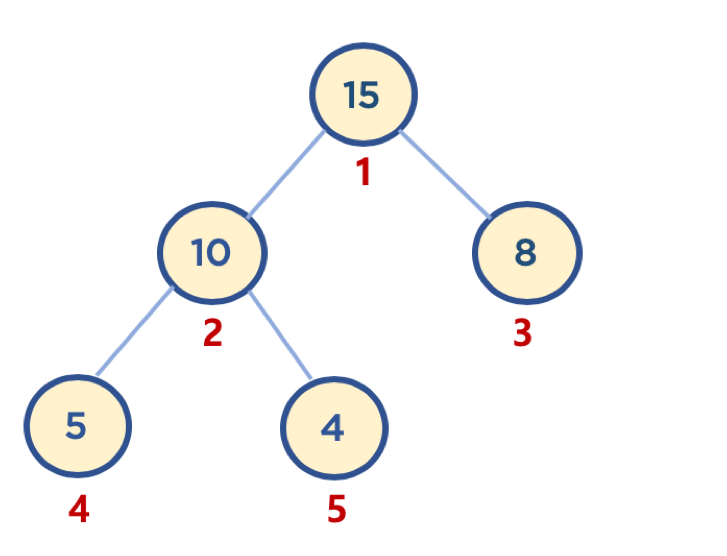
배열은 6개 인덱스 번호는 전체길이에서 -1 아니 적고보니 너무 당연한거였잖아. 힙이라 좀 다를줄
힙에 데이터 삽입 구현 (Max Heap 예)
- 힙 클래스 구현1 ``` class Heap: def init(self, data): self.heap_array = list() self.heap_array.append(None) self.heap_array.append(data)
heap = Heap(1) heap.heap_array
- 힙 클래스 구현2 - insert1
- 인덱스 번호는 1번부터 시작하도록 변경
<img src="https://www.fun-coding.org/00_Images/heap_ordinary.png">
class Heap: def init(self, data): self.heap_array = list() self.heap_array.append(None) self.heap_array.append(data)
def insert(self, data):
if len(self.heap_array) == 0:
self.heap_array.append(None)
self.heap_array.append(data)
return True
self.heap_array.append(data)#appedn가 리스트 맨 뒤에 추가
# 그 맨끝 데이터에 4번 넣게 될 것.
여기까지 데이터 넣었는데 5번 리스트 추가
이걸 append로 간단하게 구현 가능
return True ```
- 힙 클래스 구현3 - insert2
- 삽입한 노드가 부모 노드의 값보다 클 경우, 부모 노드와 삽입한 노드 위치를 바꿈
삽입한 노드가 루트 노드가 되거나, 부모 노드보다 값이 작거나 같을 경우까지 반복
- 특정 노드의 관련 노드 위치 알아내기
- 부모 노드 인덱스 번호 (parent node’s index) = 자식 노드 인덱스 번호 (child node’s index) // 2
- 왼쪽 자식 노드 인덱스 번호 (left child node’s index) = 부모 노드 인덱스 번호 (parent node’s index) * 2
- 오른쪽 자식 노드 인덱스 번호 (right child node’s index) = 부모 노드 인덱스 번호 (parent node’s index) * 2 + 1

class Heap:
def __init__(self, data):
self.heap_array = list()
self.heap_array.append(None)
self.heap_array.append(data)
def move_up(self, inserted_idx):
if inserted_idx <= 1:#이 노드가 루트노드로 갔다는 뜻
return False#루트 노드일 땐 더이상 할게 없으므로 False반환
parent_idx = inserted_idx // 2
if self.heap_array[inserted_idx] > self.heap_array[parent_idx]:
#만약 크면 그떄만 리턴해주고
return True
else:#아니면 False
return False
def insert(self, data):#이부분이 완전 이진트리에 맞춰서 배열에 데이터 넣고 append쓰면 간단히 ㄱ현가능
if len(self.heap_array) == 0:
self.heap_array.append(None)
self.heap_array.append(data)
return True
self.heap_array.append(data)
inserted_idx = len(self.heap_array) - 1#배열의 길이에 -1해줘야
while self.move_up(inserted_idx):
#부모노드에서 바꿔야 한다는 판단이 나오면
parent_idx = inserted_idx // 2
self.heap_array[inserted_idx], self.heap_array[parent_idx] = self.heap_array[parent_idx], self.heap_array[inserted_idx]
#이 부분이 swap해줬다.C언어처럼 temp변수 만들어서 안 써도 가능.(갓 파이썬)
inserted_idx = parent_idx
return True
힙에 데이터 삭제 구현 (Max Heap 예)
- 힙 클래스 구현4 - delete1
- 보통 삭제는 최상단 노드 (root 노드)를 삭제하는 것이 일반적임
- 힙의 용도는 최대값 또는 최소값을 root 노드에 놓아서, 최대값과 최소값을 바로 꺼내 쓸 수 있도록 하는 것임
class Heap:
def __init__(self, data):
self.heap_array = list()
self.heap_array.append(None)
self.heap_array.append(data)
def pop(self):
if len(self.heap_array) <= 1:
return None
returned_data = self.heap_array[1]
return returned_data
- 힙 클래스 구현4 - delete2
- 상단의 데이터 삭제시, 가장 최하단부 왼쪽에 위치한 노드 (일반적으로 가장 마지막에 추가한 노드) 를 root 노드로 이동
root 노드의 값이 child node 보다 작을 경우, root 노드의 child node 중 가장 큰 값을 가진 노드와 root 노드 위치를 바꿔주는 작업을 반복함 (swap)
- 특정 노드의 관련 노드 위치 알아내기
- 부모 노드 인덱스 번호 (parent node’s index) = 자식 노드 인덱스 번호 (child node’s index) // 2
- 왼쪽 자식 노드 인덱스 번호 (left child node’s index) = 부모 노드 인덱스 번호 (parent node’s index) * 2
- 오른쪽 자식 노드 인덱스 번호 (right child node’s index) = 부모 노드 인덱스 번호 (parent node’s index) * 2 + 1

힙 (Heap) 시간 복잡도
- depth (트리의 높이) 를 h라고 표기한다면,
- n개의 노드를 가지는 heap 에 데이터 삽입 또는 삭제시, 최악의 경우 root 노드에서 leaf 노드까지 비교해야 하므로 $h = log_2{n} $ 에 가까우므로, 시간 복잡도는 $ O(log{n}) $
- 참고: 빅오 표기법에서 $log{n}$ 에서의 log의 밑은 10이 아니라, 2입니다.
- 한번 실행시마다, 50%의 실행할 수도 있는 명령을 제거한다는 의미. 즉 50%의 실행시간을 단축시킬 수 있다는 것을 의미함